MCMC under the Hood

Dr. Mine Dogucu

The notes for this lecture are derived from Chapter 7 of the Bayes Rules! book

\(Y \sim \text{Pois}(\lambda)\)
\(\lambda \sim\text{Gamma}(1,1)\)
\(Y = 0\)

bayesrules::summarize_gamma_poisson(1, 1, sum_y = 0, n = 1)
      model shape rate mean mode  var  sd
1     prior     1    1  1.0    0 1.00 1.0
2 posterior     1    2  0.5    0 0.25 0.5

The Metropolis-Hastings algorithm

Conditioned on data \(y\), let parameter \(\lambda\) have posterior pdf \(f(\lambda | y) \propto f(\lambda) L(\lambda |y)\). A Metropolis-Hastings Markov chain for \(f(\lambda|y)\), \(\left\lbrace \lambda^{(1)}, \lambda^{(2)}, ..., \lambda^{(N)}\right\rbrace\), evolves as follows. Let \(\lambda^{(i)} = \lambda\) be the location of the chain at iteration \(i \in \{1,2,...,N-1\}\) and identify the next location \(\lambda^{(i+1)}\) through a two-step process:

Step 1: Propose a new location.
Conditioned on the current location \(\lambda\), draw a location \(\lambda'\) from a proposal model with pdf \(q(\lambda'|\lambda)\).

Step 2: Decide whether or not to go there.

Calculate the acceptance probability, ie. the probability of accepting the proposal:

\[\alpha = \min\left\lbrace 1, \; \frac{f(\lambda')L(\lambda'|y)}{f(\lambda)L(\lambda|y)} \frac{q(\lambda|\lambda')}{q(\lambda'|\lambda)} \right\rbrace\]

  • Flip a weighted coin. If it’s Heads, with probability \(\alpha\), go to the proposed location. If it’s Tails, with probability \(1 - \alpha\), stay:

    \[\lambda^{(i+1)} = \begin{cases} \lambda' & \text{ with probability } \alpha \\ \lambda & \text{ with probability } 1- \alpha \\ \end{cases}\]

current <- 1
set.seed(4)
proposal <- rnorm(1, mean = current, sd = 0.3)
proposal
[1] 1.065026

Should I stay or should I go?

proposal_plaus <- dgamma(proposal,1,1) * dpois(0,proposal)
proposal_plaus
[1] 0.118831
current_plaus  <- dgamma(current,1,1) * dpois(0,current)
current_plaus 
[1] 0.1353353

Should I stay or should I go?

alpha <- min(1, proposal_plaus / current_plaus)
alpha
[1] 0.878049

Though not certain, the probability \(\alpha\) of accepting and subsequently moving to the proposed location is relatively high

Should I stay or should I go?

To make the final determination, we flip a weighted coin which accepts the proposal with probability \(\alpha\) (0.878) and rejects the proposal with probability \(1 - \alpha\) (0.122).

next_stop <- sample(c(proposal, current), size = 1, 
  prob = c(alpha, 1-alpha))
next_stop
[1] 1.065026

one_mh_iteration <- function(sigma, current){
 # STEP 1: Propose the next chain location
 proposal <- rnorm(1, mean = current, sd = sigma)
  
 # STEP 2: Decide whether or not to go there
 if(proposal < 0) {alpha <- 0}
 else {
  proposal_plaus <- dgamma(proposal, 1, 1) * dpois(0, proposal)
  current_plaus  <- dgamma(current, 1, 1) * dpois(0, current)
  alpha <- min(1, proposal_plaus / current_plaus)
 }
 next_stop <- sample(c(proposal, current), 
  size = 1, prob = c(alpha, 1-alpha))
  
 # Return the results
 return(data.frame(proposal, alpha, next_stop))
}

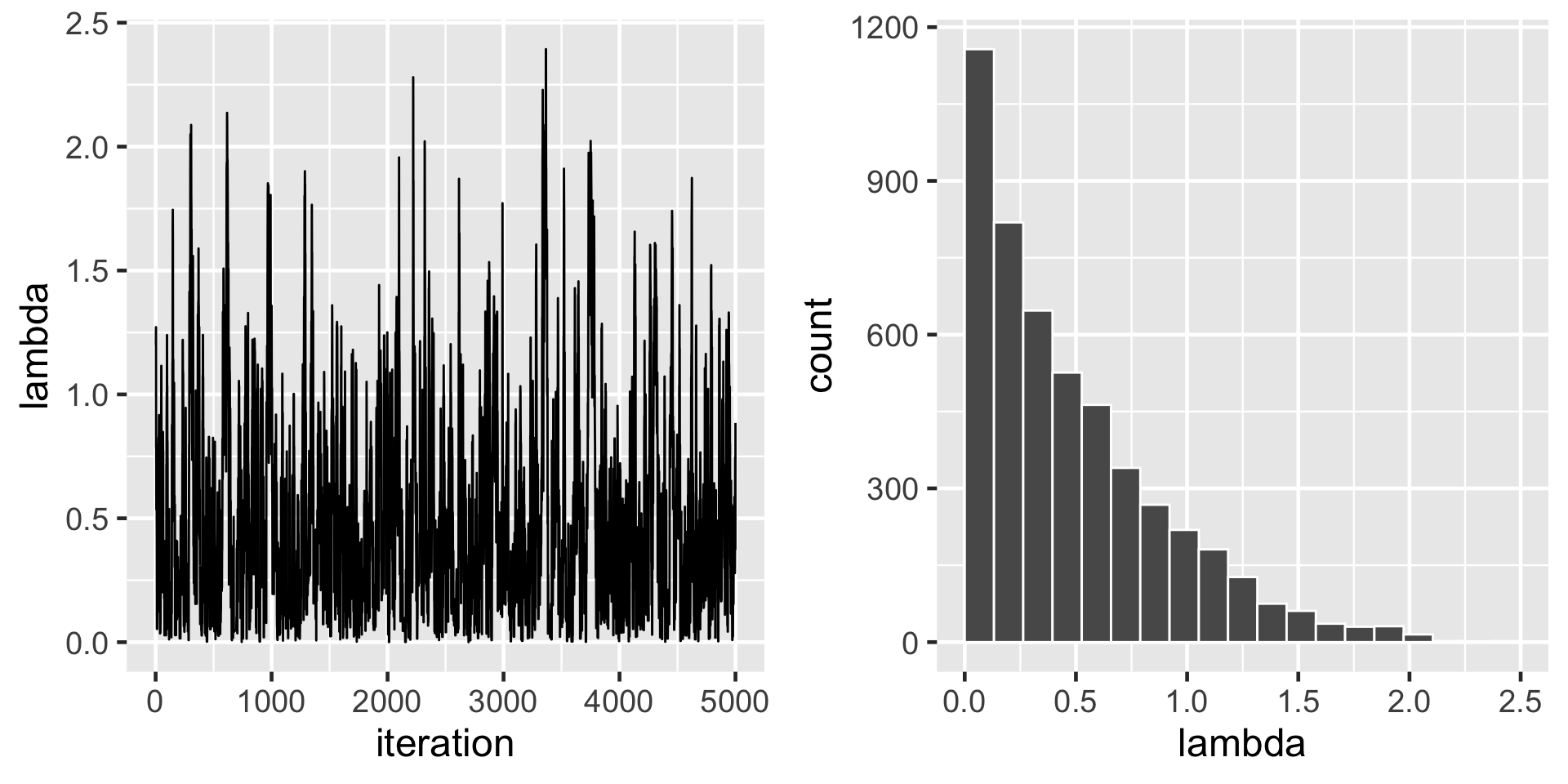
mh_tour <- function(N, sigma){
  # 1. Start the chain at location 1
  current <- 1

  # 2. Initialize the simulation
  lambda <- rep(0, N)

  # 3. Simulate N Markov chain stops
  for(i in 1:N){    
    # Simulate one iteration
    sim <- one_mh_iteration(sigma = sigma, current = current)
    
    # Record next location
    lambda[i] <- sim$next_stop
    
    # Reset the current location
    current <- sim$next_stop
  }
  
  # 4. Return the chain locations
  return(data.frame(iteration = c(1:N), lambda))
}

set.seed(4)
one_mh_iteration(sigma = 0.3, current = 1)
  proposal    alpha next_stop
1 1.065026 0.878049  1.065026
set.seed(7)
one_mh_iteration(sigma = 0.3, current = 1)
  proposal     alpha next_stop
1 1.686174 0.2535109         1
set.seed(84735)
mh_simulation_1 <- mh_tour(N = 5000, sigma = 0.3)

ggplot(mh_simulation_1, aes(x = iteration, y = lambda)) + 
  geom_line()

ggplot(mh_simulation_1, aes(x = lambda)) + 
  geom_histogram(color = "white")

stats115.com