Posterior Inference and Prediction

Dr. Mine Dogucu

The notes for this lecture are derived from Chapter 8 of the Bayes Rules! book

library(bayesrules)
data(moma_sample)
glimpse(moma_sample)
Rows: 100
Columns: 10
$ artist            <fct> Ad Gerritsen, Kirstine Roepstorff, Lisa Baumgardner,…
$ country           <fct> dutch, danish, american, american, american, canadia…
$ birth             <fct> 1940, 1972, 1958, 1952, 1946, 1927, 1901, 1941, 1920…
$ death             <fct> 2015, NA, 2015, NA, NA, 1966, 1971, NA, 2007, NA, NA…
$ alive             <lgl> FALSE, TRUE, FALSE, TRUE, TRUE, FALSE, FALSE, TRUE, …
$ genx              <lgl> FALSE, TRUE, FALSE, FALSE, FALSE, FALSE, FALSE, FALS…
$ gender            <fct> male, female, female, male, male, male, male, male, …
$ count             <int> 1, 3, 2, 1, 1, 8, 2, 1, 1, 5, 1, 2, 1, 1, 21, 16, 1,…
$ year_acquired_min <fct> 1981, 2005, 2016, 2001, 2012, 2008, 2018, 1981, 1949…
$ year_acquired_max <fct> 1981, 2005, 2016, 2001, 2012, 2008, 2018, 1981, 1949…

\[Y|\pi \sim \text{Bin}(100, \pi)\]

\[\pi \sim \text{Beta}(4, 6)\]

moma_sample |> 
  group_by(genx) |> 
  tally()
# A tibble: 2 × 2
  genx      n
  <lgl> <int>
1 FALSE    86
2 TRUE     14

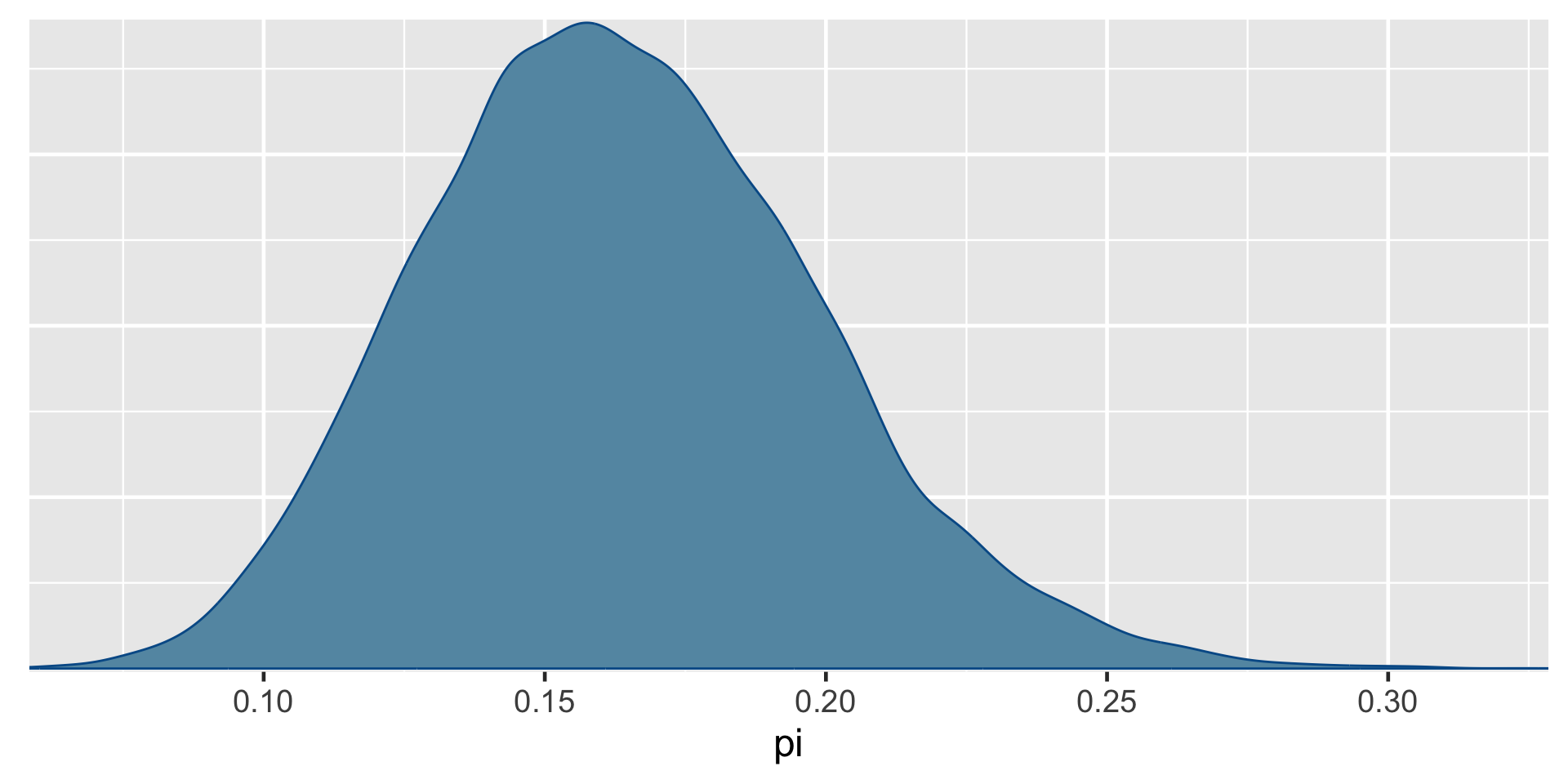
\[\begin{split} Y | \pi & \sim \text{Bin}(100, \pi) \\ \pi & \sim \text{Beta}(4, 6) \\ \end{split} \;\;\;\; \Rightarrow \;\;\;\; \pi | (Y = 14) \sim \text{Beta}(18, 92)\]

plot_beta_binomial(alpha = 4, beta = 6, y = 14, n = 100)

summarize_beta_binomial(4, 6, y = 14, n = 100)
      model alpha beta      mean      mode         var         sd
1     prior     4    6 0.4000000 0.3750000 0.021818182 0.14770979
2 posterior    18   92 0.1636364 0.1574074 0.001232969 0.03511365

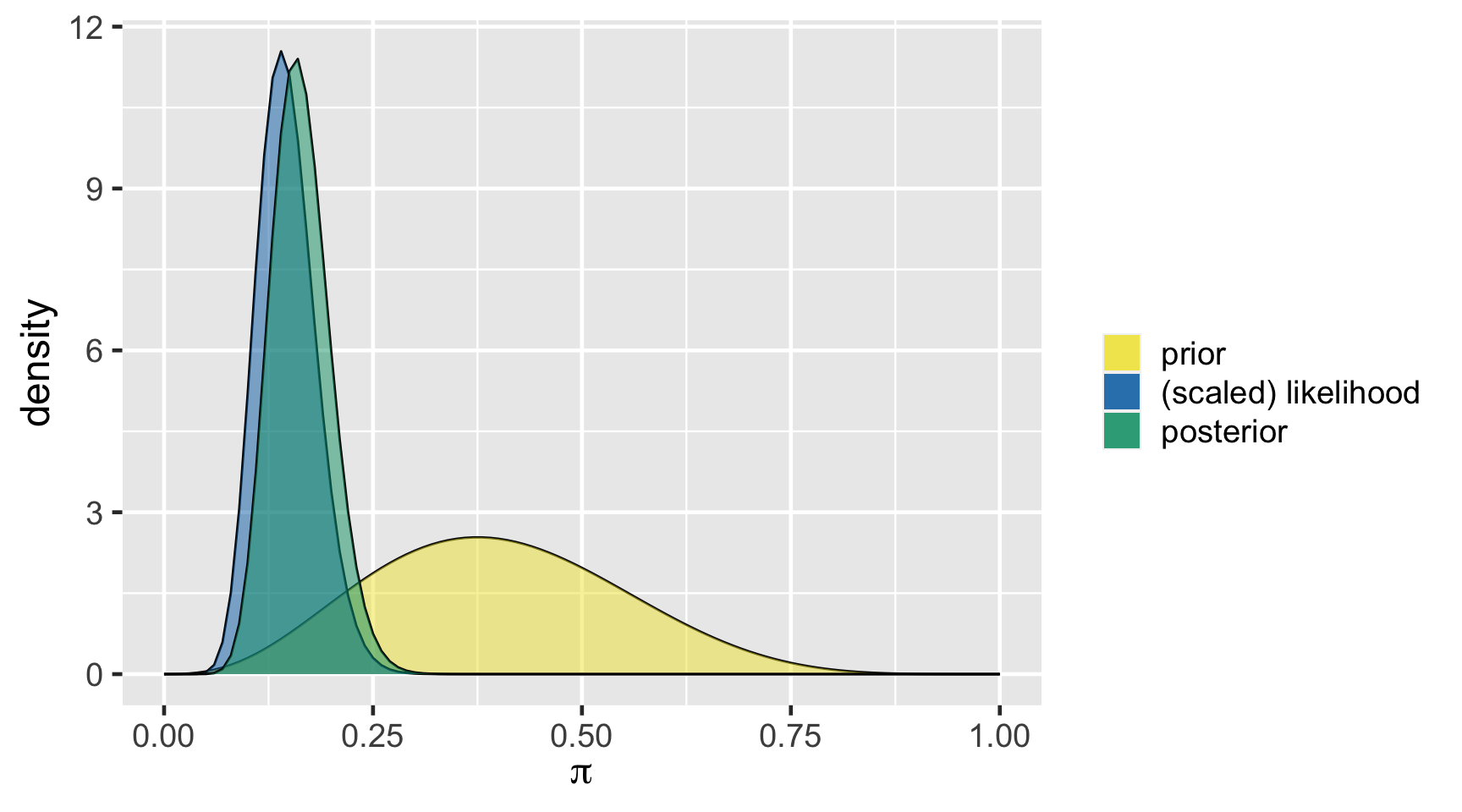
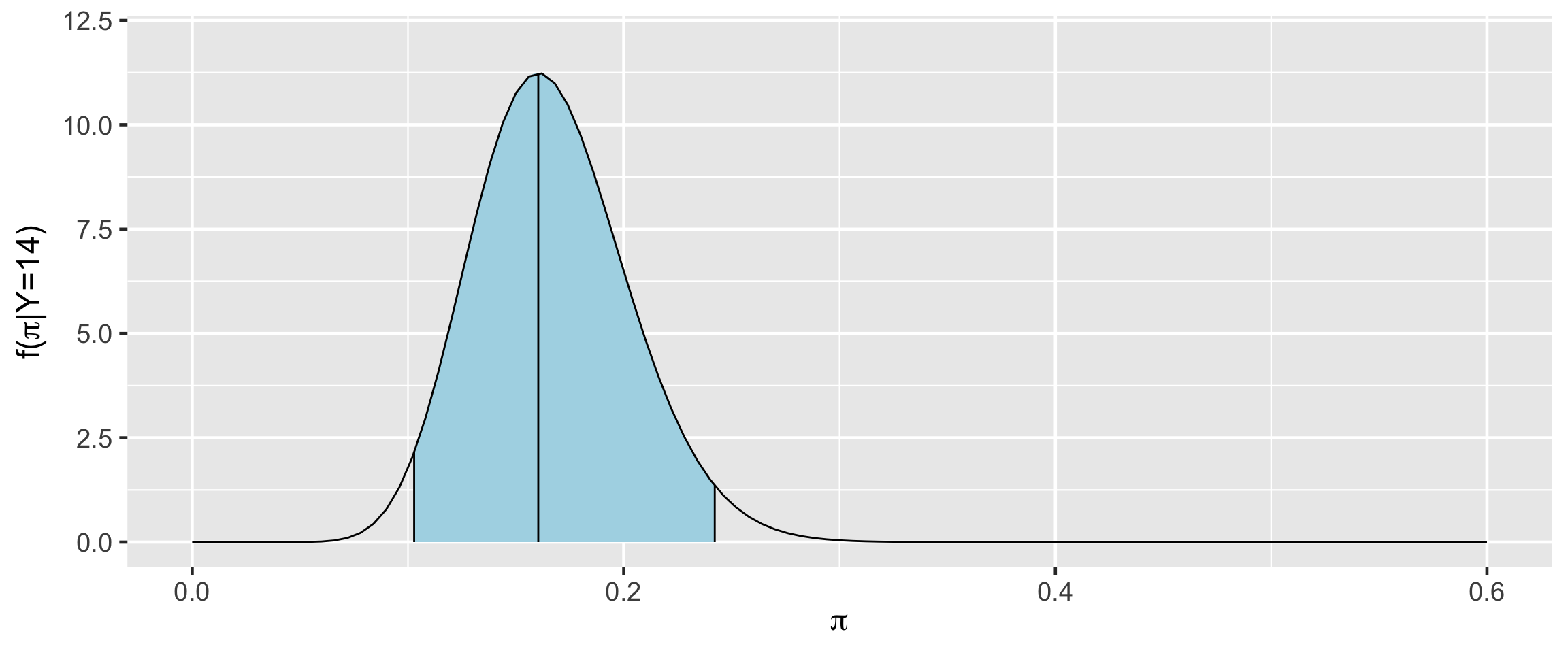
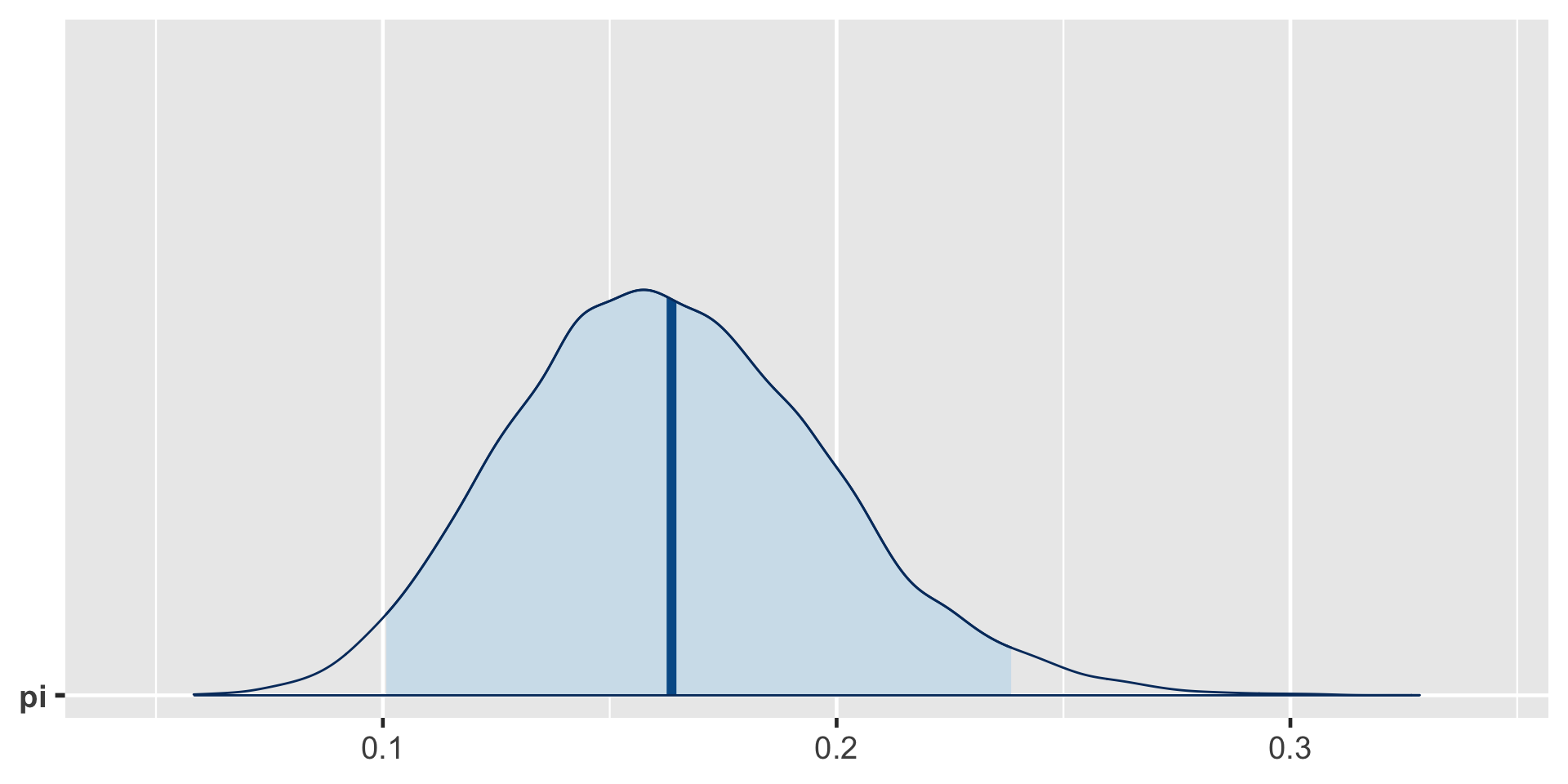
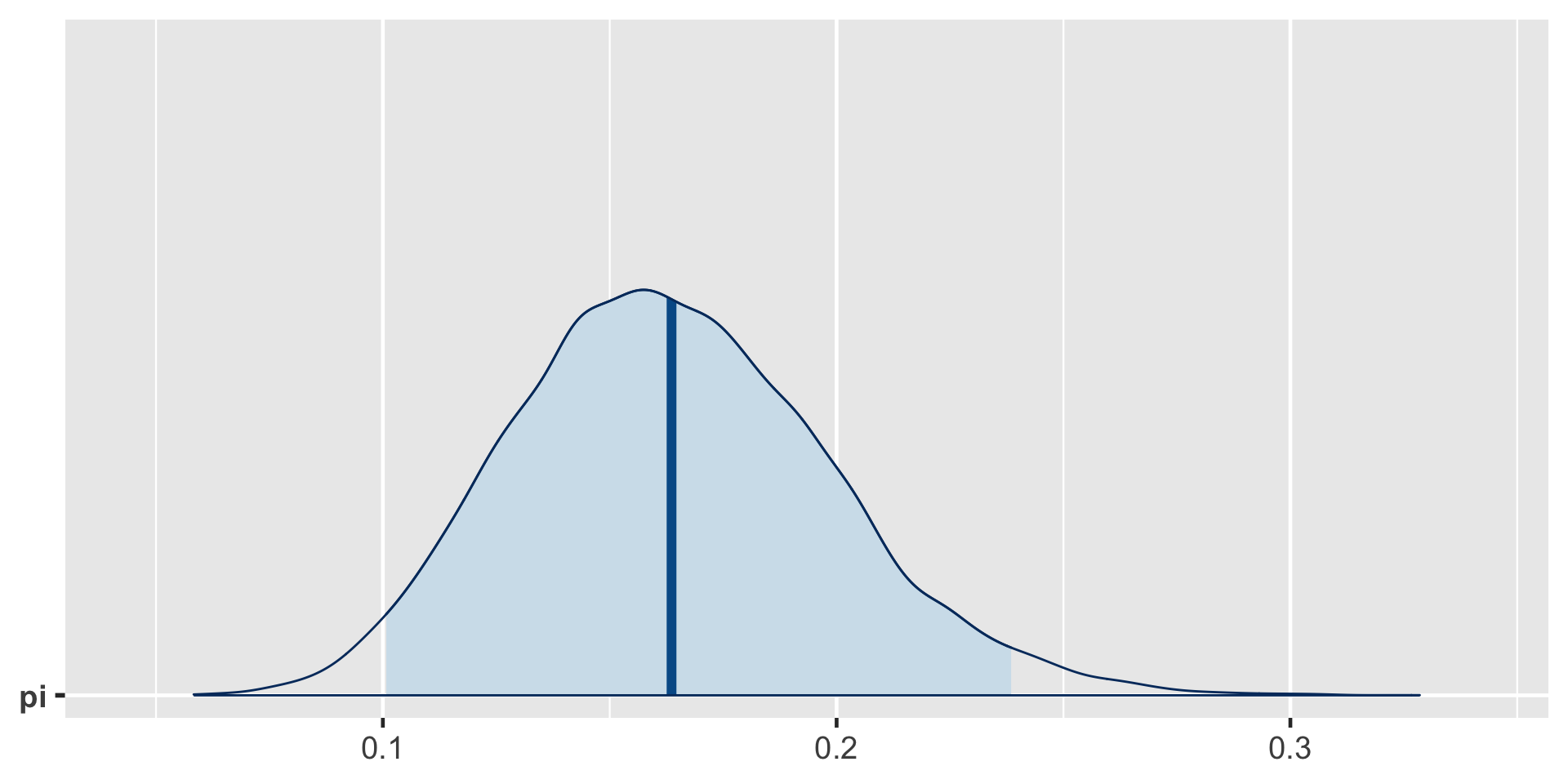
95% Posterior Credible Interval (CI)

0.025th & 0.975th quantiles of the Beta(18,92) posterior

qbeta(c(0.025, 0.975), 18, 92)
[1] 0.1009084 0.2379286

\(\int_{0.1}^{0.24} f(\pi|(y=14)) d\pi \; \approx \; 0.95\)

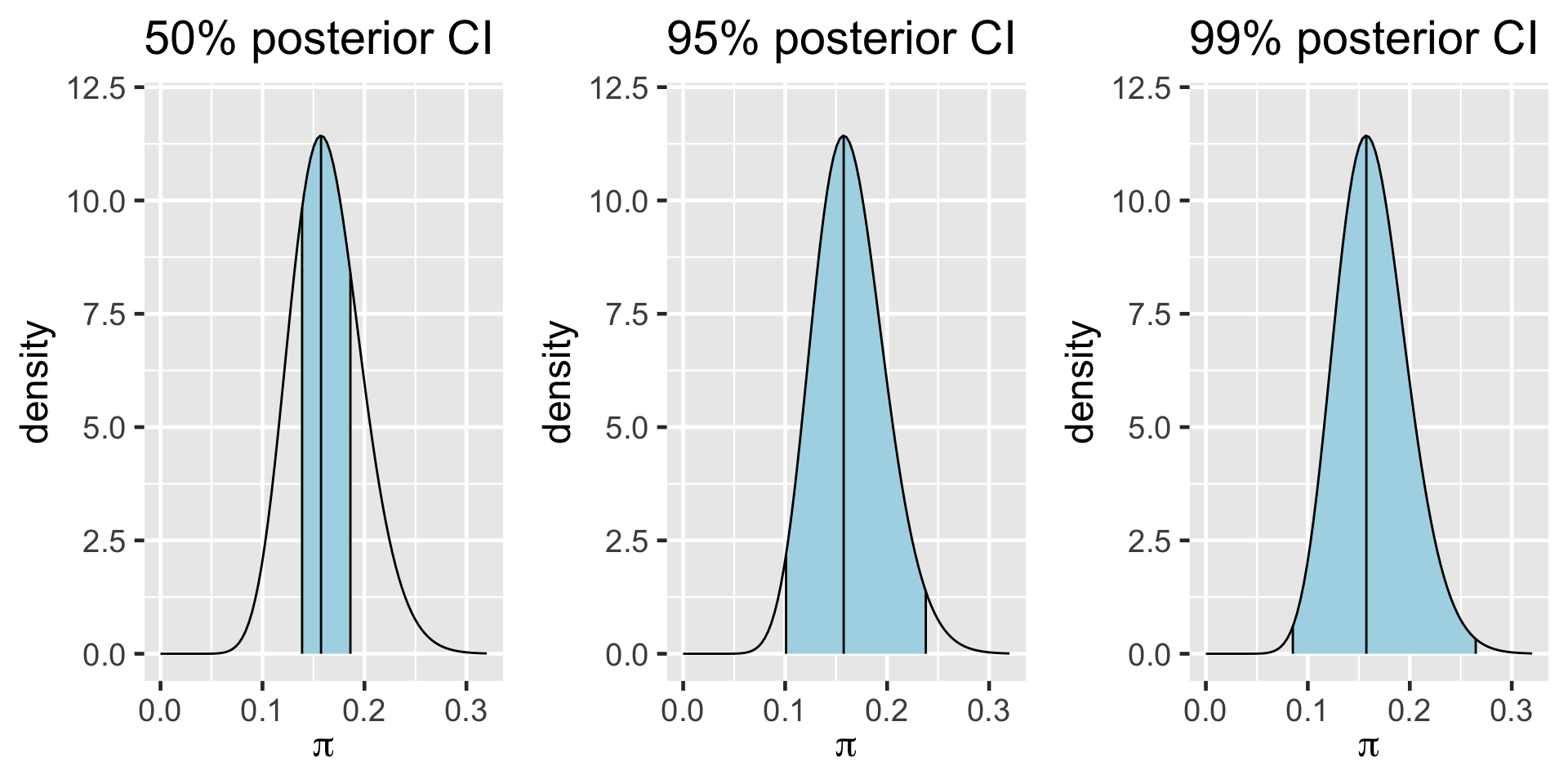
\[\begin{split} H_0: & \; \; \pi \ge 0.20 \\ H_a: & \; \; \pi < 0.20 \\ \end{split}\]

# Posterior probability that pi < 0.20
post_prob <- pbeta(0.20, 18, 92)
post_prob
[1] 0.8489856

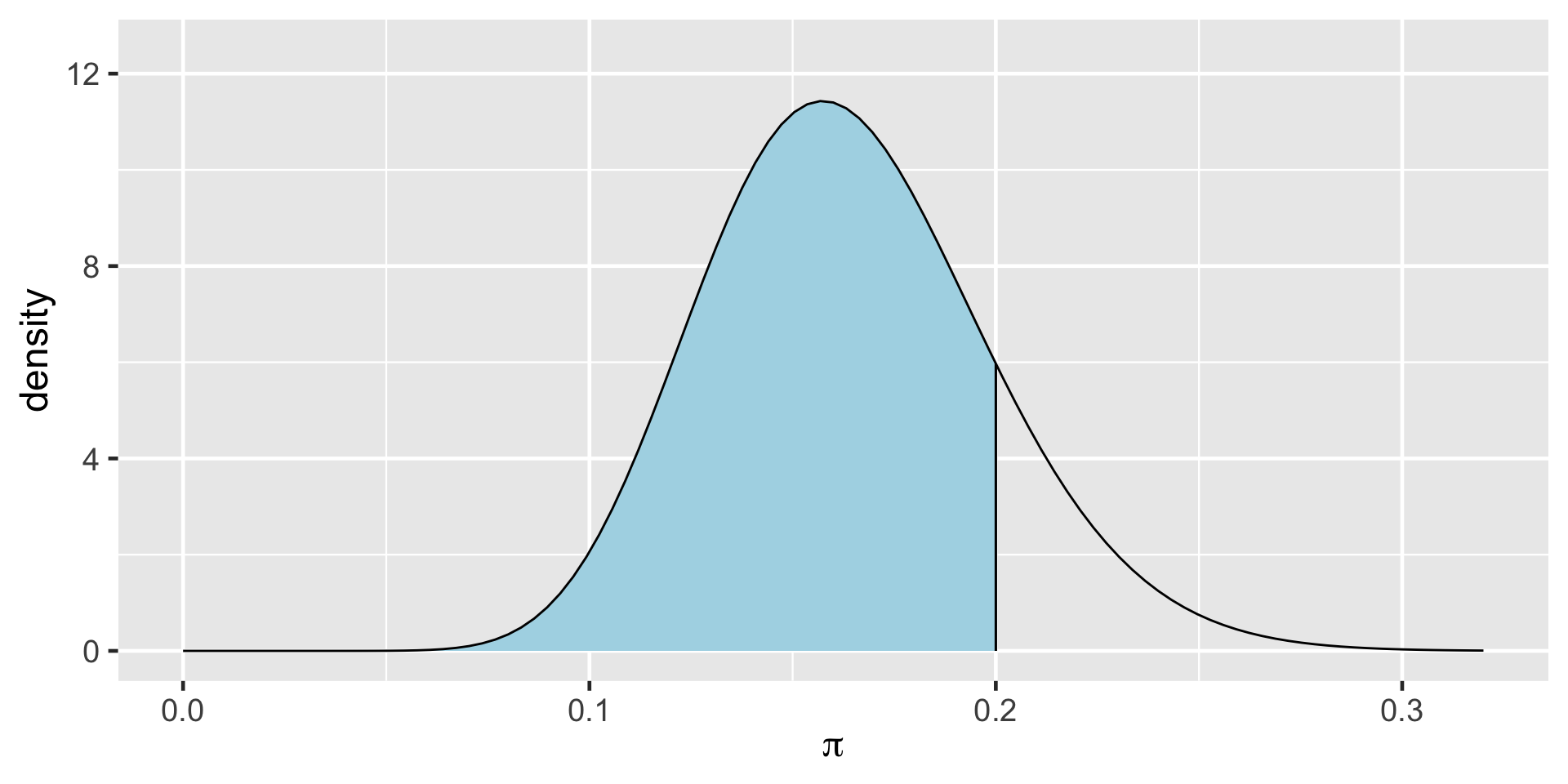
\[\text{Posterior odds } = \frac{P(H_a \; | \; (Y=14))}{P(H_0 \; | \; (Y=14))} \approx 5.62 \]

# Posterior odds
post_odds <- post_prob / (1 - post_prob)
post_odds
[1] 5.621883

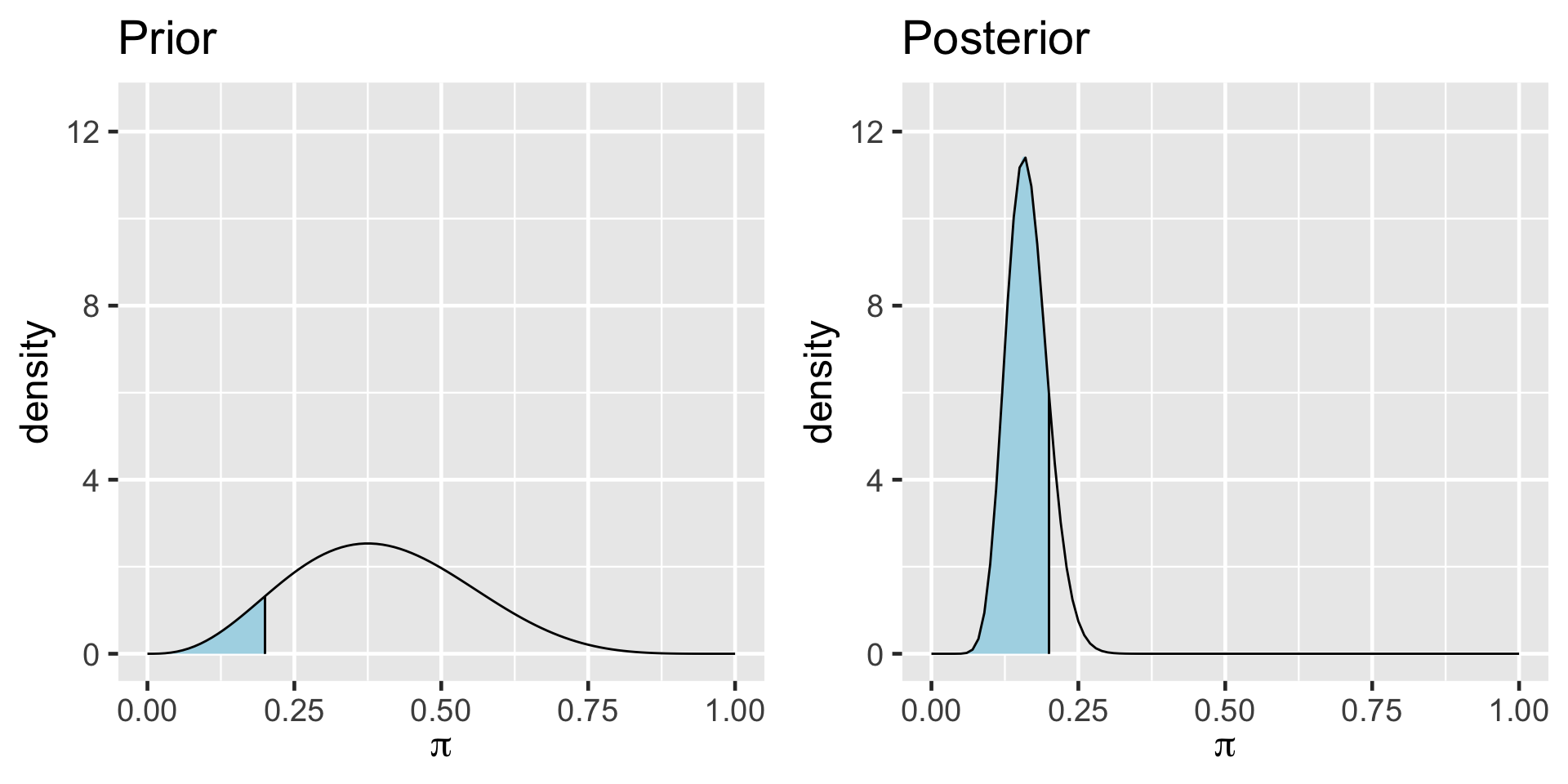
\[P(\pi<0.20)\]

prior_prob <- pbeta(0.20, 4, 6)
prior_prob
[1] 0.08564173

\[\text{Prior odds } = \frac{P(H_a)}{P(H_0)} \approx 0.093 \; .\]

prior_odds <- prior_prob / (1 - prior_prob)
prior_odds
[1] 0.09366321

The Bayes Factor (BF) compares the posterior odds to the prior odds, hence provides insight into just how much our understanding about Gen X representation evolved upon observing our sample data:

\[\text{Bayes Factor} = \frac{\text{Posterior odds }}{\text{Prior odds }}\]

Bayes Factor

In a hypothesis test of two competing hypotheses, \(H_a\) vs \(H_0\), the Bayes Factor is an odds ratio for \(H_a\):

\[\text{Bayes Factor} = \frac{\text{Posterior odds}}{\text{Prior odds}} = \frac{P(H_a | Y) / P(H_0 | Y)}{P(H_a) / P(H_0)} \; .\]

As a ratio, it’s meaningful to compare the Bayes Factor (BF) to 1. To this end, consider three possible scenarios:

  1. BF = 1: The plausibility of \(H_a\) didn’t change in light of the observed data.
  2. BF > 1: The plausibility of \(H_a\) increased in light of the observed data. Thus the greater the Bayes Factor, the more convincing the evidence for \(H_a\).
  3. BF < 1: The plausibility of \(H_a\) decreased in light of the observed data.

Two-sided Tests

\[\begin{split} H_0: & \; \; \pi = 0.3 \\ H_a: & \; \; \pi \ne 0.3 \\ \end{split}\]

\[\text{Posterior odds } = \frac{P(H_a \; | \; (Y=14))}{P(H_0 \; | \; (Y=14))} = \frac{1}{0} = \text{ nooooo!}\]

Recall 95% posterior CI

qbeta(c(0.025, 0.975), 18, 92)
[1] 0.1009084 0.2379286

library(rstan)
# STEP 1: DEFINE the model
art_model <- "
  data {
    int<lower=0, upper=100> Y;
  }
  parameters {
    real<lower=0, upper=1> pi;
  }
  model {
    Y ~ binomial(100, pi);
    pi ~ beta(4, 6);
  }
"
# STEP 2: SIMULATE the posterior
art_sim <- stan(model_code = art_model, data = list(Y = 14), 
  chains = 4, iter = 5000*2, seed = 84735)

SAMPLING FOR MODEL 'anon_model' NOW (CHAIN 1).
Chain 1: 
Chain 1: Gradient evaluation took 1.1e-05 seconds
Chain 1: 1000 transitions using 10 leapfrog steps per transition would take 0.11 seconds.
Chain 1: Adjust your expectations accordingly!
Chain 1: 
Chain 1: 
Chain 1: Iteration:    1 / 10000 [  0%]  (Warmup)
Chain 1: Iteration: 1000 / 10000 [ 10%]  (Warmup)
Chain 1: Iteration: 2000 / 10000 [ 20%]  (Warmup)
Chain 1: Iteration: 3000 / 10000 [ 30%]  (Warmup)
Chain 1: Iteration: 4000 / 10000 [ 40%]  (Warmup)
Chain 1: Iteration: 5000 / 10000 [ 50%]  (Warmup)
Chain 1: Iteration: 5001 / 10000 [ 50%]  (Sampling)
Chain 1: Iteration: 6000 / 10000 [ 60%]  (Sampling)
Chain 1: Iteration: 7000 / 10000 [ 70%]  (Sampling)
Chain 1: Iteration: 8000 / 10000 [ 80%]  (Sampling)
Chain 1: Iteration: 9000 / 10000 [ 90%]  (Sampling)
Chain 1: Iteration: 10000 / 10000 [100%]  (Sampling)
Chain 1: 
Chain 1:  Elapsed Time: 0.027 seconds (Warm-up)
Chain 1:                0.027 seconds (Sampling)
Chain 1:                0.054 seconds (Total)
Chain 1: 

SAMPLING FOR MODEL 'anon_model' NOW (CHAIN 2).
Chain 2: 
Chain 2: Gradient evaluation took 1e-06 seconds
Chain 2: 1000 transitions using 10 leapfrog steps per transition would take 0.01 seconds.
Chain 2: Adjust your expectations accordingly!
Chain 2: 
Chain 2: 
Chain 2: Iteration:    1 / 10000 [  0%]  (Warmup)
Chain 2: Iteration: 1000 / 10000 [ 10%]  (Warmup)
Chain 2: Iteration: 2000 / 10000 [ 20%]  (Warmup)
Chain 2: Iteration: 3000 / 10000 [ 30%]  (Warmup)
Chain 2: Iteration: 4000 / 10000 [ 40%]  (Warmup)
Chain 2: Iteration: 5000 / 10000 [ 50%]  (Warmup)
Chain 2: Iteration: 5001 / 10000 [ 50%]  (Sampling)
Chain 2: Iteration: 6000 / 10000 [ 60%]  (Sampling)
Chain 2: Iteration: 7000 / 10000 [ 70%]  (Sampling)
Chain 2: Iteration: 8000 / 10000 [ 80%]  (Sampling)
Chain 2: Iteration: 9000 / 10000 [ 90%]  (Sampling)
Chain 2: Iteration: 10000 / 10000 [100%]  (Sampling)
Chain 2: 
Chain 2:  Elapsed Time: 0.027 seconds (Warm-up)
Chain 2:                0.029 seconds (Sampling)
Chain 2:                0.056 seconds (Total)
Chain 2: 

SAMPLING FOR MODEL 'anon_model' NOW (CHAIN 3).
Chain 3: 
Chain 3: Gradient evaluation took 1e-06 seconds
Chain 3: 1000 transitions using 10 leapfrog steps per transition would take 0.01 seconds.
Chain 3: Adjust your expectations accordingly!
Chain 3: 
Chain 3: 
Chain 3: Iteration:    1 / 10000 [  0%]  (Warmup)
Chain 3: Iteration: 1000 / 10000 [ 10%]  (Warmup)
Chain 3: Iteration: 2000 / 10000 [ 20%]  (Warmup)
Chain 3: Iteration: 3000 / 10000 [ 30%]  (Warmup)
Chain 3: Iteration: 4000 / 10000 [ 40%]  (Warmup)
Chain 3: Iteration: 5000 / 10000 [ 50%]  (Warmup)
Chain 3: Iteration: 5001 / 10000 [ 50%]  (Sampling)
Chain 3: Iteration: 6000 / 10000 [ 60%]  (Sampling)
Chain 3: Iteration: 7000 / 10000 [ 70%]  (Sampling)
Chain 3: Iteration: 8000 / 10000 [ 80%]  (Sampling)
Chain 3: Iteration: 9000 / 10000 [ 90%]  (Sampling)
Chain 3: Iteration: 10000 / 10000 [100%]  (Sampling)
Chain 3: 
Chain 3:  Elapsed Time: 0.026 seconds (Warm-up)
Chain 3:                0.027 seconds (Sampling)
Chain 3:                0.053 seconds (Total)
Chain 3: 

SAMPLING FOR MODEL 'anon_model' NOW (CHAIN 4).
Chain 4: 
Chain 4: Gradient evaluation took 1e-06 seconds
Chain 4: 1000 transitions using 10 leapfrog steps per transition would take 0.01 seconds.
Chain 4: Adjust your expectations accordingly!
Chain 4: 
Chain 4: 
Chain 4: Iteration:    1 / 10000 [  0%]  (Warmup)
Chain 4: Iteration: 1000 / 10000 [ 10%]  (Warmup)
Chain 4: Iteration: 2000 / 10000 [ 20%]  (Warmup)
Chain 4: Iteration: 3000 / 10000 [ 30%]  (Warmup)
Chain 4: Iteration: 4000 / 10000 [ 40%]  (Warmup)
Chain 4: Iteration: 5000 / 10000 [ 50%]  (Warmup)
Chain 4: Iteration: 5001 / 10000 [ 50%]  (Sampling)
Chain 4: Iteration: 6000 / 10000 [ 60%]  (Sampling)
Chain 4: Iteration: 7000 / 10000 [ 70%]  (Sampling)
Chain 4: Iteration: 8000 / 10000 [ 80%]  (Sampling)
Chain 4: Iteration: 9000 / 10000 [ 90%]  (Sampling)
Chain 4: Iteration: 10000 / 10000 [100%]  (Sampling)
Chain 4: 
Chain 4:  Elapsed Time: 0.027 seconds (Warm-up)
Chain 4:                0.028 seconds (Sampling)
Chain 4:                0.055 seconds (Total)
Chain 4: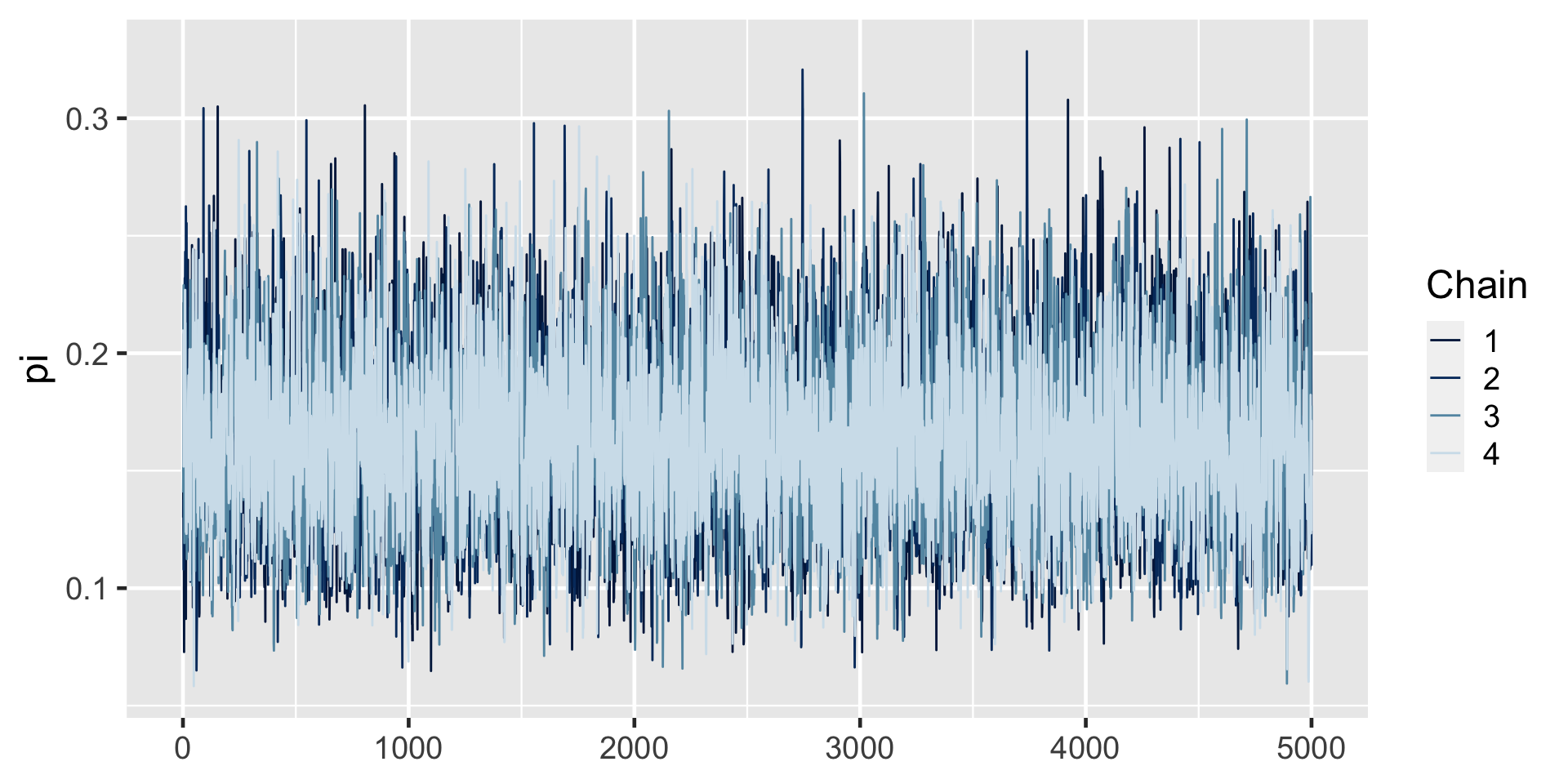 

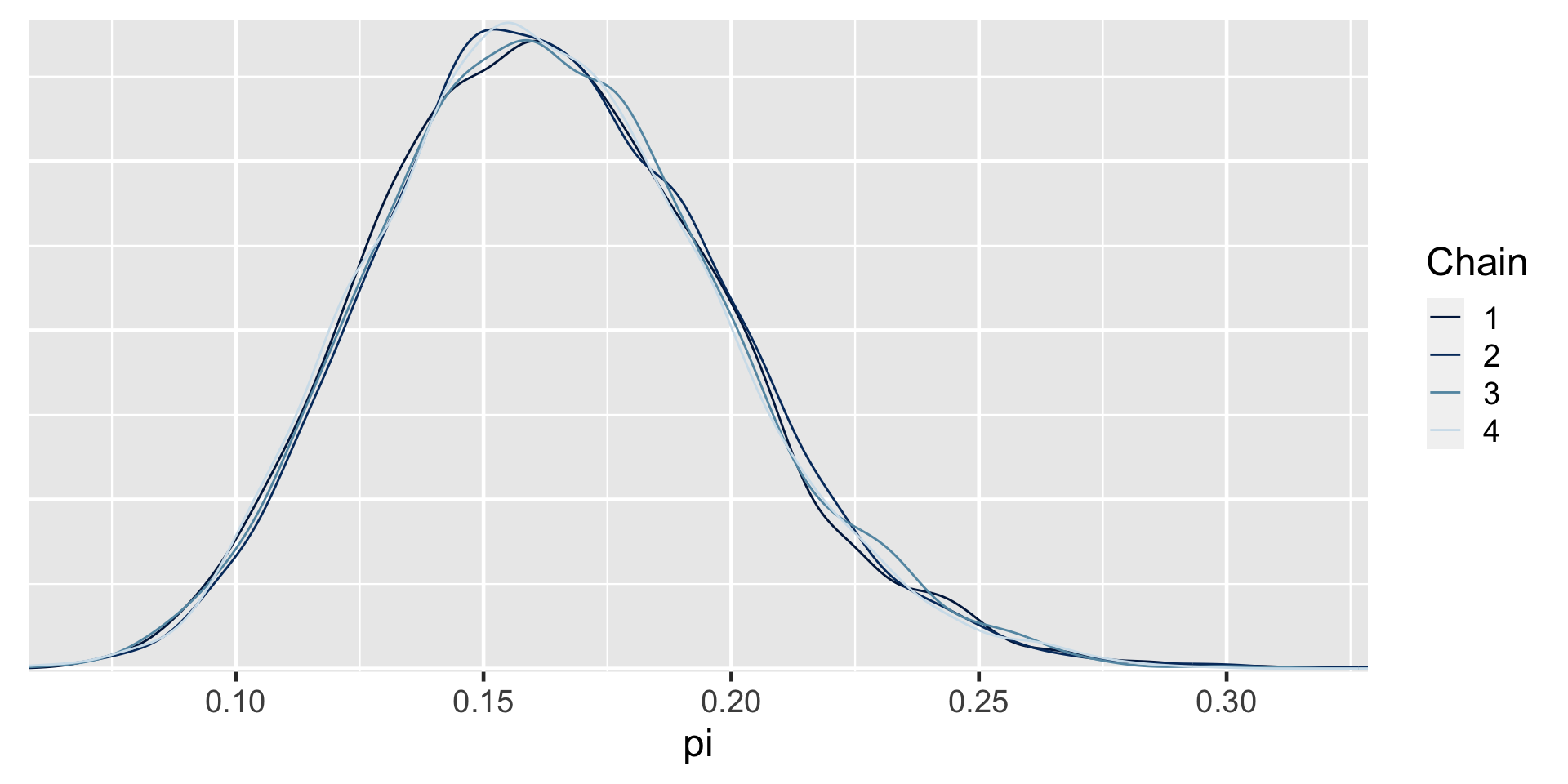
library(bayesplot)
# Parallel trace plots & density plots
mcmc_trace(art_sim, pars = "pi", size = 0.5)

# Combined density plot
mcmc_dens_overlay(art_sim, pars = "pi")

# Combined density plot
mcmc_dens(art_sim, pars = "pi")

summary(art_sim, pars = "pi")

mcmc_areas(art_sim, pars = "pi",
  prob = 0.95, point_est = "mean")

mcmc_areas(art_sim, pars = "pi",
  prob = 0.95, point_est = "mean")

art_chains_df <- as.data.frame(art_sim, 
  pars ="lp__", include = FALSE)

art_chains_df |> 
  summarize(post_mean = mean(pi), 
    post_mode = sample_mode(pi),
    lower_95 = quantile(pi, 0.025),
    upper_95 = quantile(pi, 0.975))
  post_mean post_mode  lower_95  upper_95
1 0.1636757 0.1577523 0.1007598 0.2384584

art_chains_df |> 
  mutate(exceeds = pi < 0.20) |> 
  tabyl(exceeds)
 exceeds     n percent
   FALSE  2987 0.14935
    TRUE 17013 0.85065
post_prob
[1] 0.8489856

a Bayesian analysis assesses the uncertainty regarding an unknown parameter \(\pi\) in light of observed data \(Y\).

\[P((\pi < 0.20) \; | \; (Y = 14)) = 0.8489856 \;.\]

a frequentist analysis assesses the uncertainty of the observed data \(Y\) in light of assumed values of \(\pi\).

\[P((Y \le 14) | (\pi = 0.20)) = 0.08\]

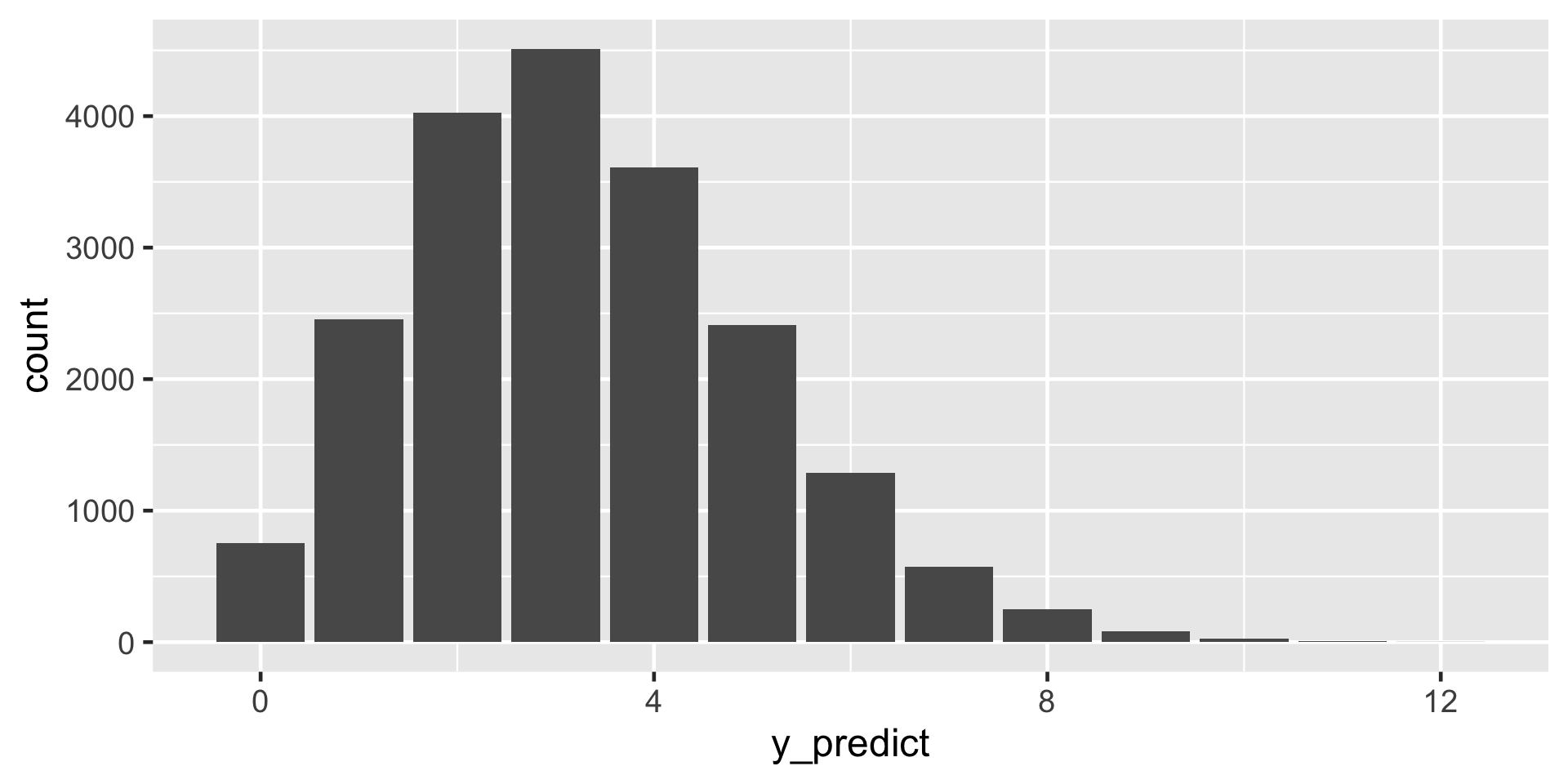
Posterior prediction of new outcomes

Suppose we get our hands on 20 more artworks. What number would you predict are done by artists that are Gen X or younger?

  • sampling variability

  • posterior variability in \(\pi\).

First, let \(Y' = y'\) be the (yet unknown) number of the 20 new artworks that are done by Gen X or younger artists. Thus conditioned on \(\pi\), the randomness in \(Y'\) can be modeled by \(Y'|\pi \sim \text{Bin}(20,\pi)\) with pdf

\[f(y'|\pi) = P(Y' = y' | \pi) = \binom{20}{ y'} \pi^{y'}(1-\pi)^{20 - y'}\]

\[f(y'|\pi) f(\pi|(y=14)) \; ,\]

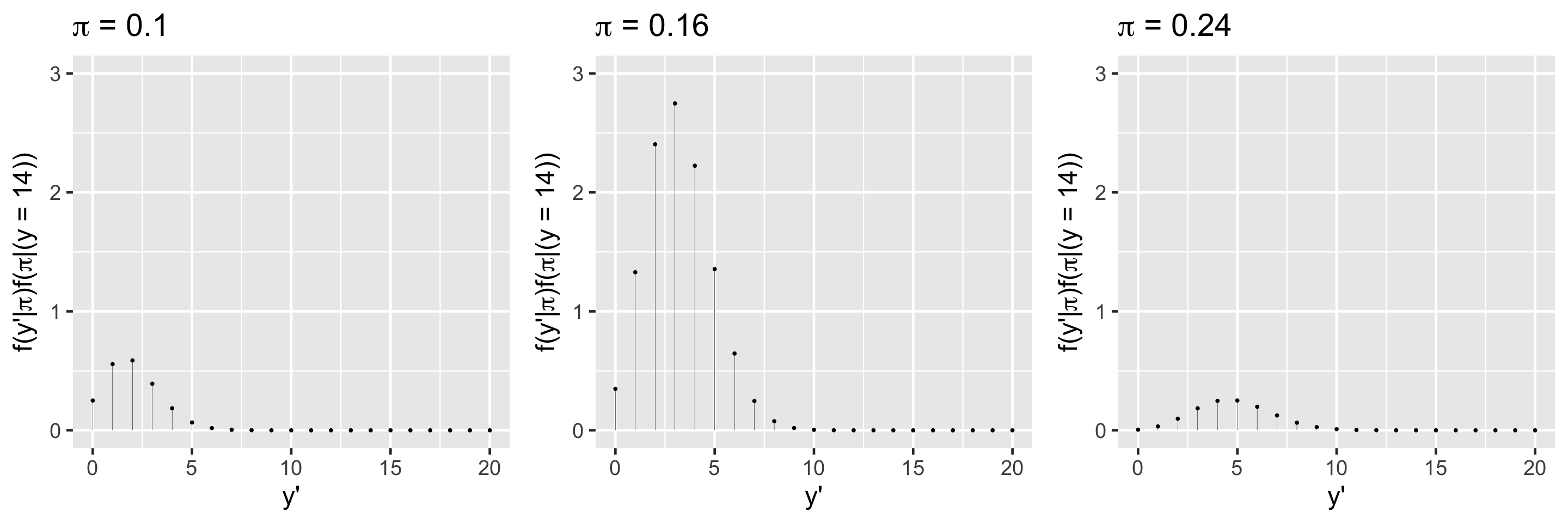
\(f(y'|(y=14)) = \int_0^1 f(y'|\pi) f(\pi|(y=14)) d\pi\)

\(f(y'|(y=14)) = {20 \choose y'} \frac{\Gamma(110)}{\Gamma(18)\Gamma(92)}\frac{\Gamma(18+y')\Gamma(112-y')} {\Gamma(130)} \text{ for } y' \in \{0,1,\ldots,20\}\)

\(f((y'=3)|(y=14)) = {20 \choose 3}\frac{\Gamma(110)}{\Gamma(18)\Gamma(92)}\frac{\Gamma(18+3)\Gamma(112-3)} {\Gamma(130)} = 0.2217\)

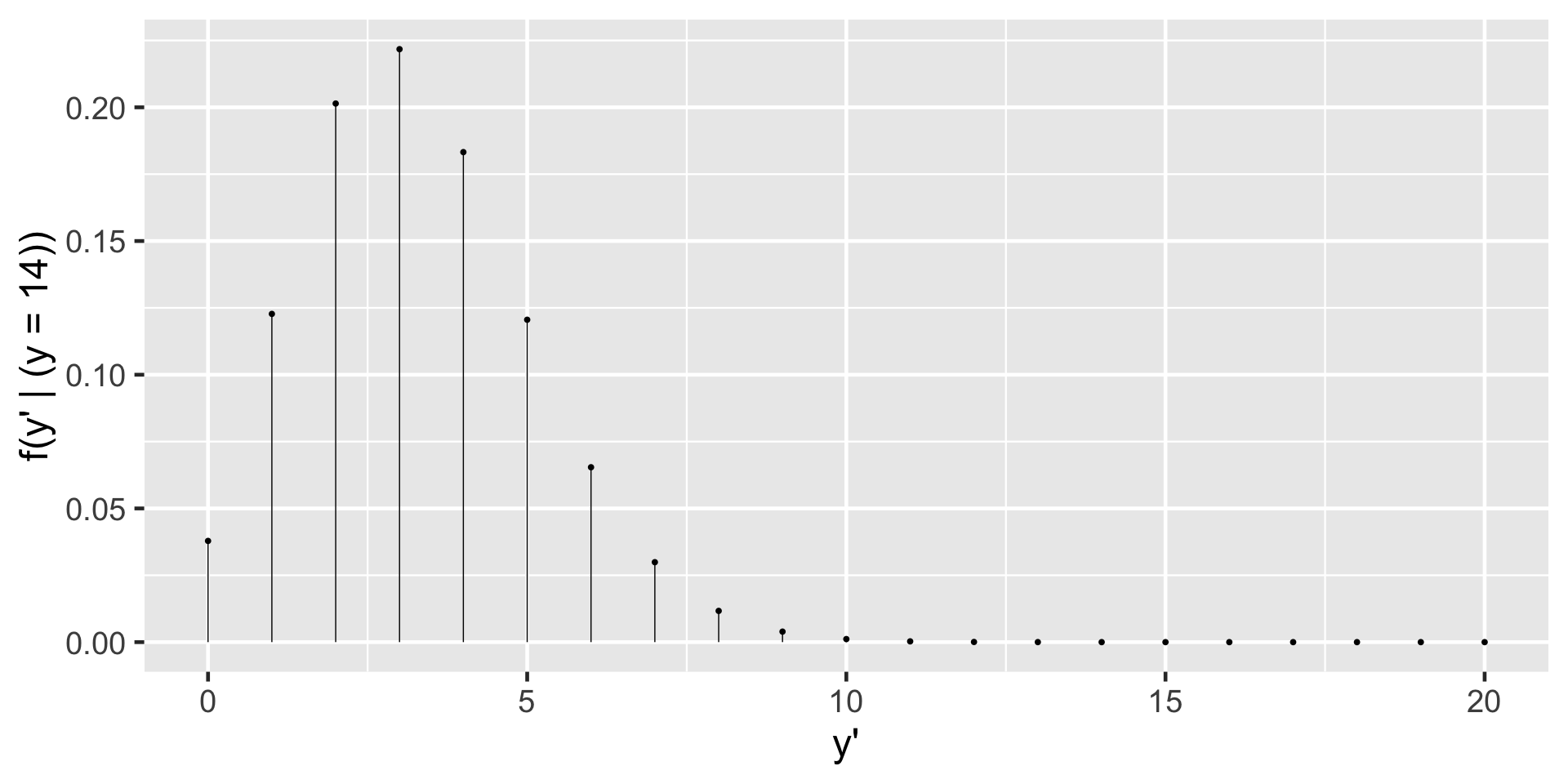
Let \(Y'\) denote a new outcome of variable \(Y\). Further, let pdf \(f(y'|\pi)\) denote the dependence of \(Y'\) on \(\pi\) and posterior pdf \(f(\pi|y)\) denote the posterior plausibility of \(\pi\) given the original data \(Y = y\). Then the posterior predictive model for \(Y'\) has pdf

\[f(y'|y) = \int f(y'|\pi) f(\pi|y) d\pi \; .\]

In words, the overall chance of observing \(Y' = y'\) weights the chance of observing this outcome under any possible \(\pi\) ( \(f(y'|\pi)\) ) by the posterior plausibility of \(\pi\) ( \(f(\pi|y)\) ).

head(art_chains_df, 3)
         pi
1 0.1300701
2 0.1755285
3 0.2214175

set.seed(84735)
# Predict a value of Y' for each pi value in the chain
art_chains_df <- art_chains_df |> 
  mutate(y_predict = rbinom(length(pi), size = 20, prob = pi))
head(art_chains_df, 3)
         pi y_predict
1 0.1300701         4
2 0.1755285         4
3 0.2214175         4

ggplot(art_chains_df, aes(x = y_predict)) + 
  stat_count()

stats115.com