Simple Normal Regression

Dr. Mine Dogucu

The notes for this lecture are derived from Chapter 9 of the Bayes Rules! book

glimpse(bikes)
Rows: 500
Columns: 13
$ date        <date> 2011-01-01, 2011-01-03, 2011-01-04, 2011-01-05, 2011-01-0…
$ season      <fct> winter, winter, winter, winter, winter, winter, winter, wi…
$ year        <int> 2011, 2011, 2011, 2011, 2011, 2011, 2011, 2011, 2011, 2011…
$ month       <fct> Jan, Jan, Jan, Jan, Jan, Jan, Jan, Jan, Jan, Jan, Jan, Jan…
$ day_of_week <fct> Sat, Mon, Tue, Wed, Fri, Sat, Mon, Tue, Wed, Thu, Fri, Sat…
$ weekend     <lgl> TRUE, FALSE, FALSE, FALSE, FALSE, TRUE, FALSE, FALSE, FALS…
$ holiday     <fct> no, no, no, no, no, no, no, no, no, no, no, no, no, yes, n…
$ temp_actual <dbl> 57.39952, 46.49166, 46.76000, 48.74943, 46.50332, 44.17700…
$ temp_feel   <dbl> 64.72625, 49.04645, 51.09098, 52.63430, 50.79551, 46.60286…
$ humidity    <dbl> 80.5833, 43.7273, 59.0435, 43.6957, 49.8696, 53.5833, 48.2…
$ windspeed   <dbl> 10.749882, 16.636703, 10.739832, 12.522300, 11.304642, 17.…
$ weather_cat <fct> categ2, categ1, categ1, categ1, categ2, categ2, categ1, ca…
$ rides       <int> 654, 1229, 1454, 1518, 1362, 891, 1280, 1220, 1137, 1368, …

Rides

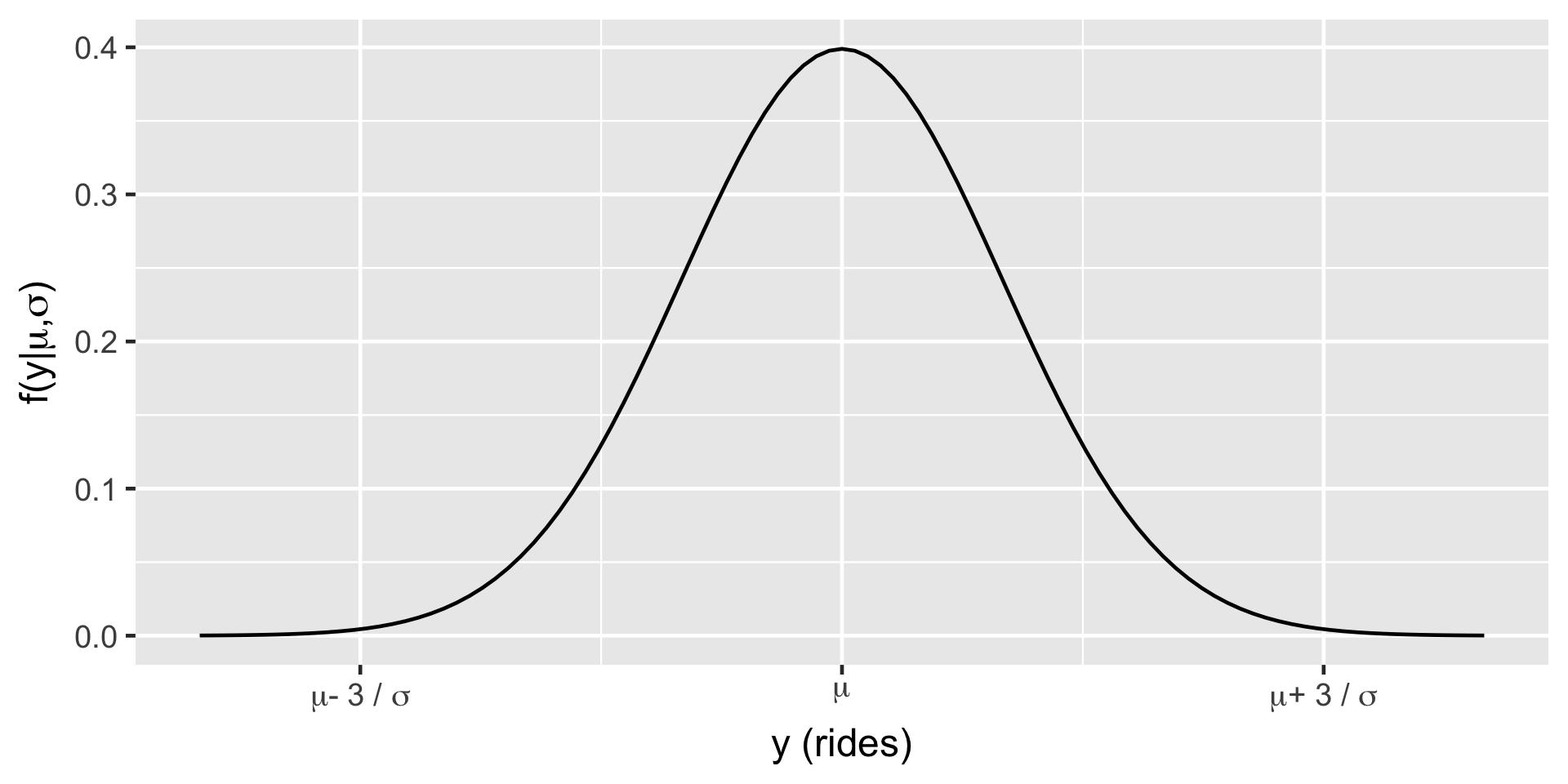
\(Y_i | \mu, \sigma \stackrel{ind}{\sim} N(\mu, \sigma^2)\)
\(\mu \sim N(\theta, \tau^2)\) \(\sigma \sim \text{ some prior model.}\)

Regression Model

\(Y_i\) the number of rides
\(X_i\) temperature (in Fahrenheit) on day \(i\).

\(\mu_i = \beta_0 + \beta_1X_i\)

\(\beta_0:\) the typical ridership on days in which the temperature was 0 degrees ( \(X_i\)=0). It is not interpretable in this case.

\(\beta_1:\) the typical change in ridership for every one unit increase in temperature.

Normal likelihood model

\[\begin{split} Y_i | \beta_0, \beta_1, \sigma & \stackrel{ind}{\sim} N\left(\mu_i, \sigma^2\right) \;\; \text{ with } \;\; \mu_i = \beta_0 + \beta_1X_i \; .\\ \end{split}\]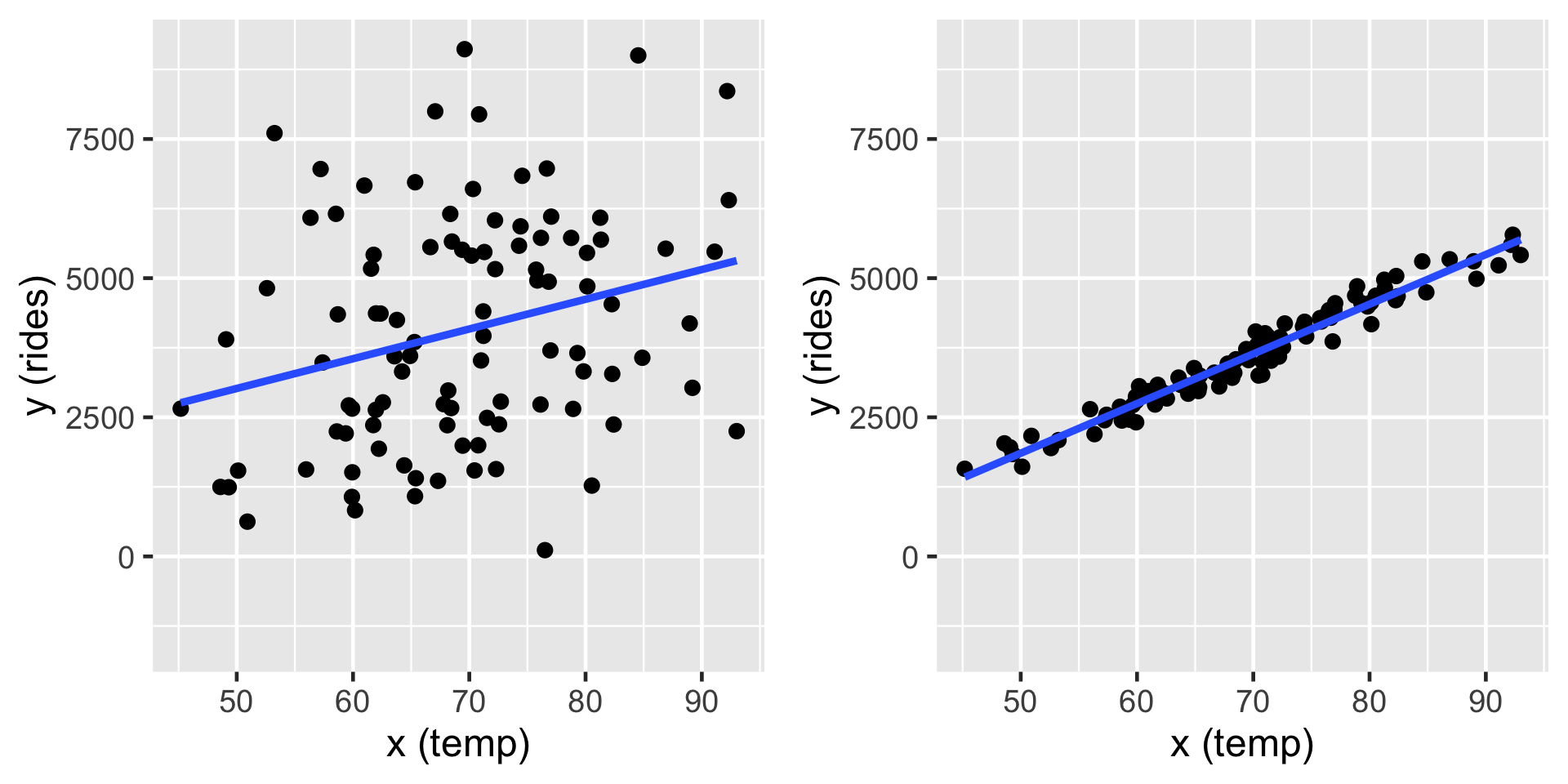

These simulations show two cases where \(\beta_0 = -2000\) and slope \(\beta_1 = 100\). On the left \(\sigma = 2000\) and on the right \(\sigma = 200\) (right). In both cases, the model line is defined by \(\beta_0 + \beta_1 x = -2000 + 100 x\).

Prior Models

\(\text{likelihood model:} \; \; \; Y_i | \beta_0, \beta_1, \sigma \;\;\;\stackrel{ind}{\sim} N\left(\mu_i, \sigma^2\right)\text{ with } \mu_i = \beta_0 + \beta_1X_i\)

\(\text{prior models:}\)

\(\beta_0\sim N(m_0, s_0^2 )\)
\(\beta_1\sim N(m_1, s_1^2 )\)
\(\sigma \sim \text{Exp}(l)\)

Recall:

\(\text{Exp}(l) = \text{Gamma}(1, l)\)

plot_normal(mean = 5000, sd = 1000) + 
  labs(x = "beta_0c", y = "pdf")

plot_normal(mean = 100, sd = 40) + 
  labs(x = "beta_1", y = "pdf")

plot_gamma(shape = 1, rate = 0.0008) + 
  labs(x = "sigma", y = "pdf")

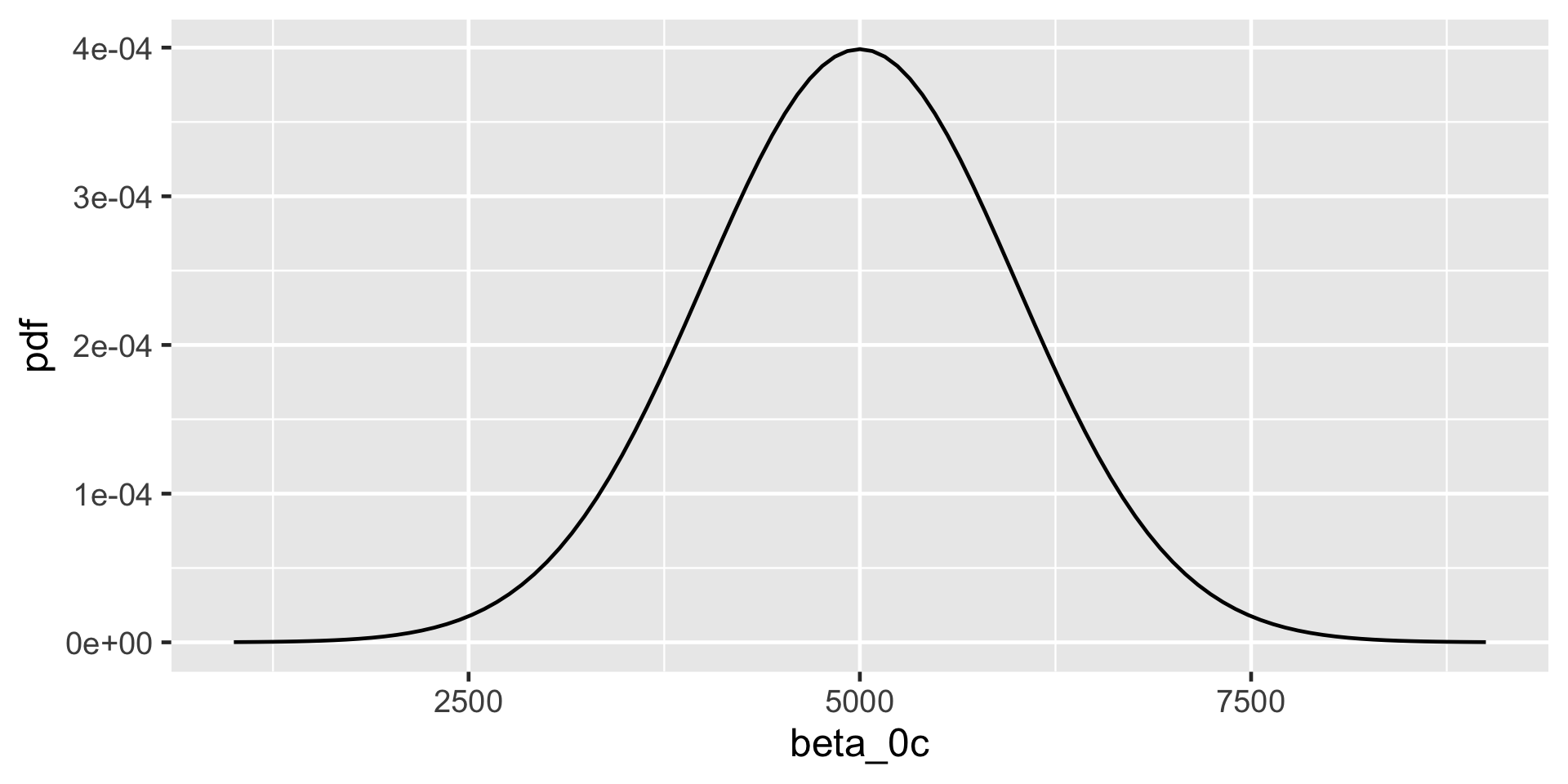
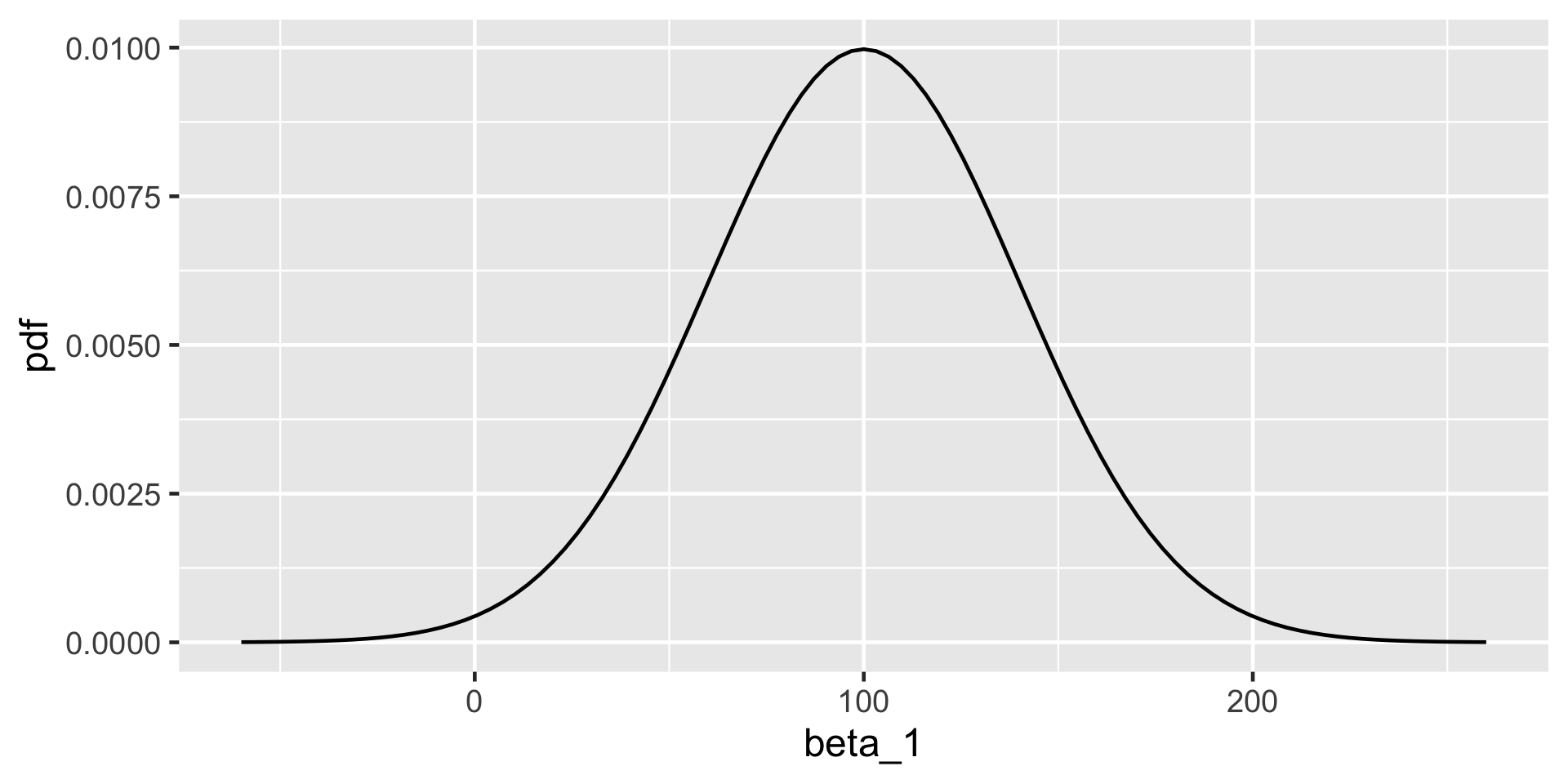
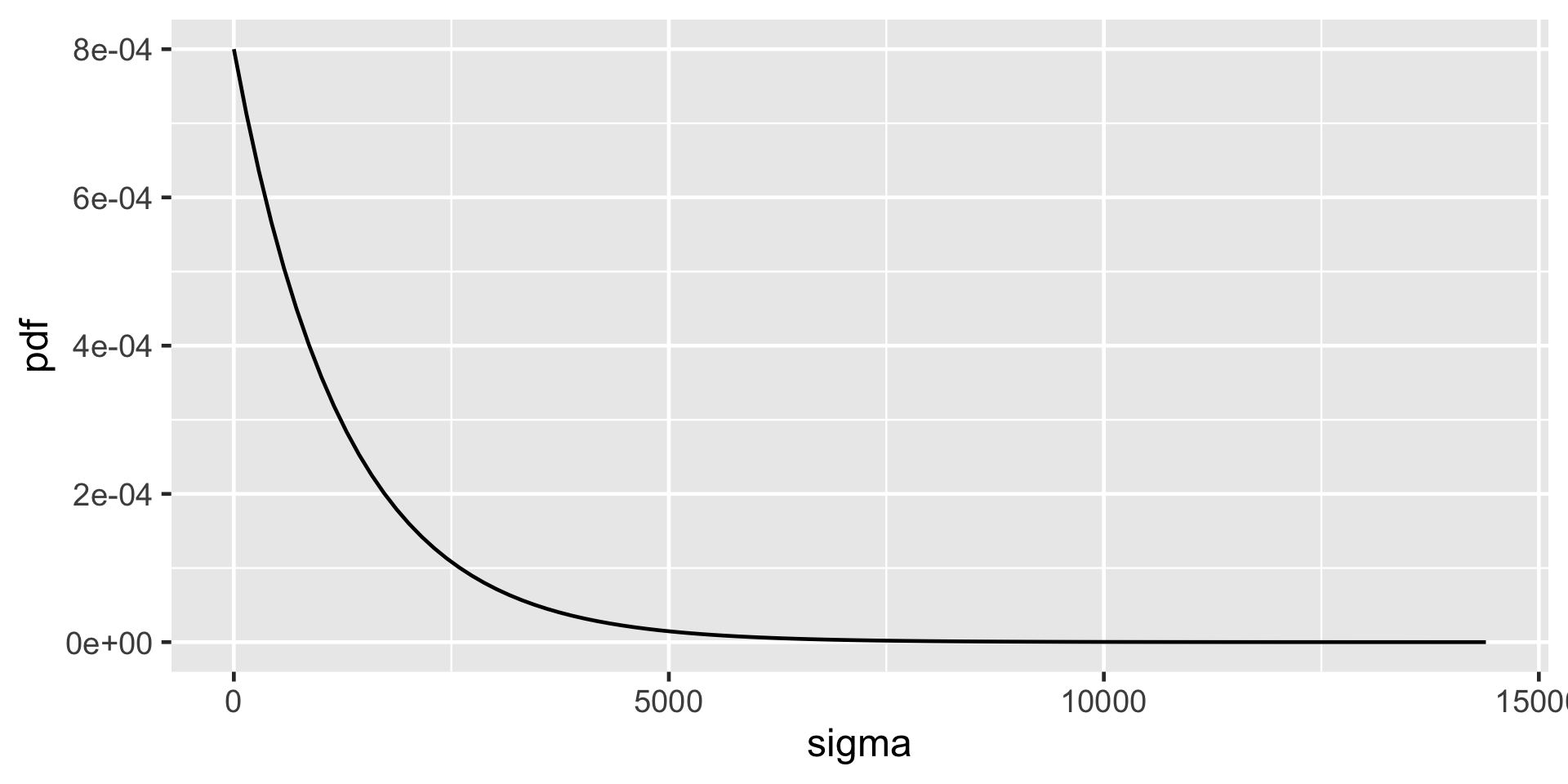
\[\begin{split} Y_i | \beta_0, \beta_1, \sigma & \stackrel{ind}{\sim} N\left(\mu_i, \sigma^2\right) \;\; \text{ with } \;\; \mu_i = \beta_0 + \beta_1X_i \\ \beta_{0c} & \sim N\left(5000, 1000^2 \right) \\ \beta_1 & \sim N\left(100, 40^2 \right) \\ \sigma & \sim \text{Exp}(0.0008) .\\ \end{split}\]

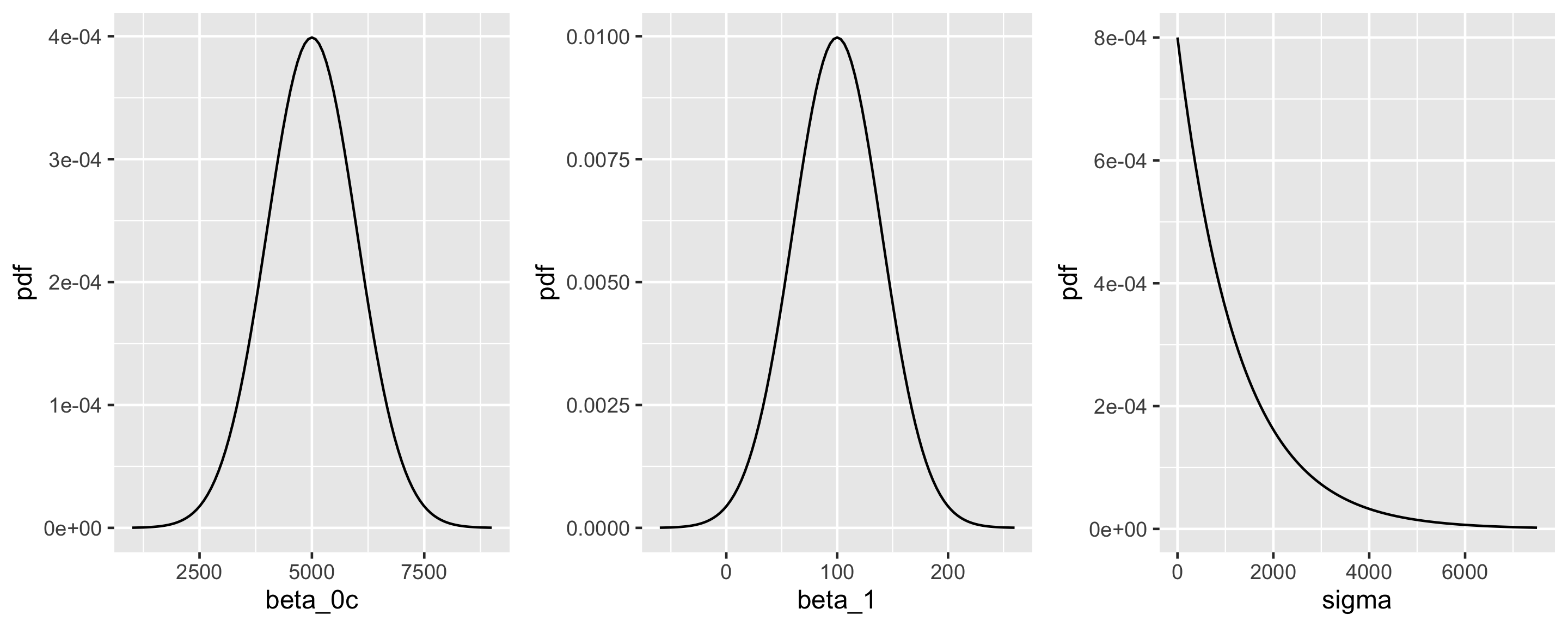
Simulation via rstanarm

bike_model <- stan_glm(rides ~ temp_feel, data = bikes,
                       family = gaussian,
                       prior_intercept = normal(5000, 1000),
                       prior = normal(100, 40), 
                       prior_aux = exponential(0.0008),
                       chains = 4, iter = 5000*2, seed = 84735,
                       refresh = FALSE)

The refresh = FALSE prevents printing out your chains and iterations, especially useful in R Markdown.

# Effective sample size ratio and Rhat
neff_ratio(bike_model)
(Intercept)   temp_feel       sigma 
    1.03285     1.03505     0.96585 
rhat(bike_model)
(Intercept)   temp_feel       sigma 
  0.9998873   0.9999032   0.9999642

The effective sample size ratios are slightly above 1 and the R-hat values are very close to 1, indicating that the chains are stable, mixing quickly, and behaving much like an independent sample.

mcmc_trace(bike_model, size = 0.1)

mcmc_dens_overlay(bike_model)

# STEP 1: DEFINE the model
stan_bike_model <- "
  data {
    int<lower = 0> n;
    vector[n] Y;
    vector[n] X;
  }
  parameters {
    real beta0;
    real beta1;
    real<lower = 0> sigma;
  }
  model {
    Y ~ normal(beta0 + beta1 * X, sigma);
    beta0 ~ normal(-2000, 1000);
    beta1 ~ normal(100, 40);
    sigma ~ exponential(0.0008);
  }
"

# STEP 2: SIMULATE the posterior
stan_bike_sim <- 
  stan(model_code = stan_bike_model, 
       data = list(n = nrow(bikes), Y = bikes$rides, X = bikes$temp_feel), 
       chains = 4, iter = 5000*2, seed = 84735, refresh = FALSE)

broom.mixed::tidy(bike_model, effects = c("fixed", "aux"),
     conf.int = TRUE, conf.level = 0.80)
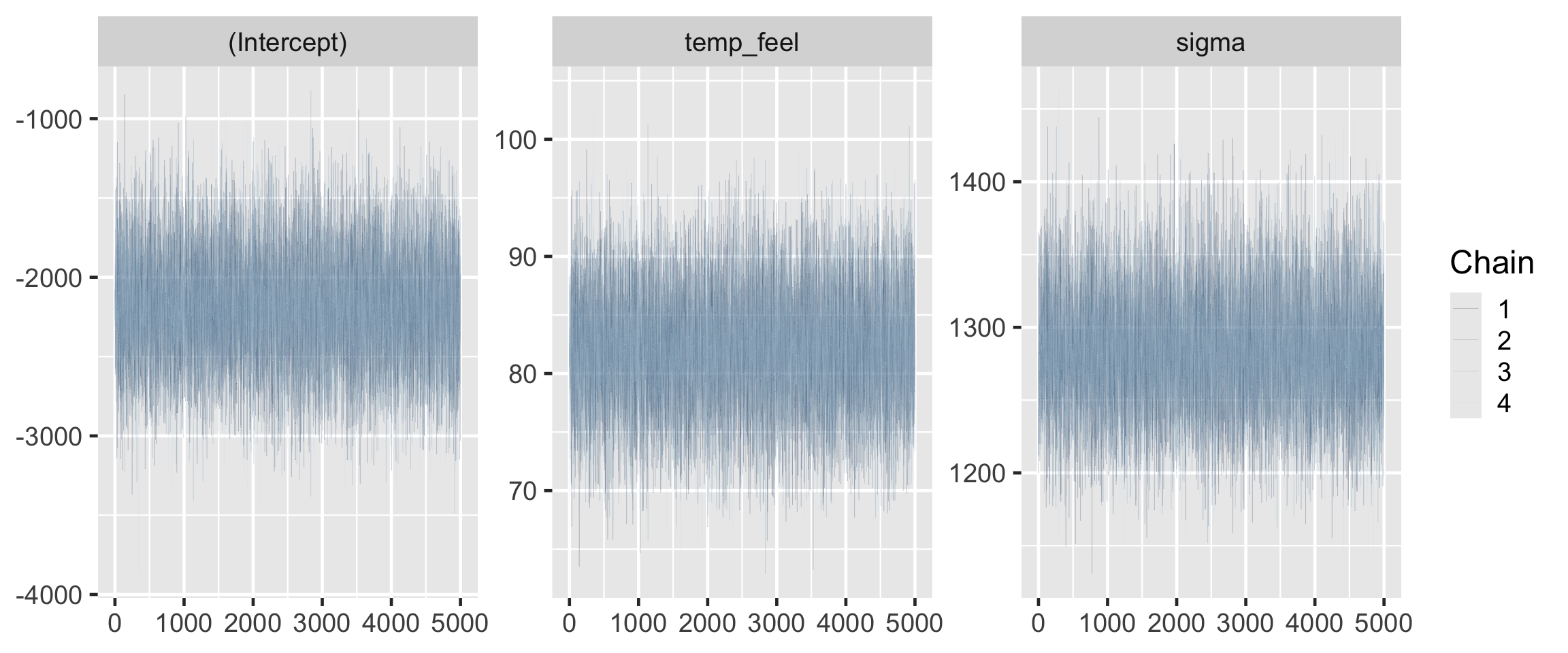
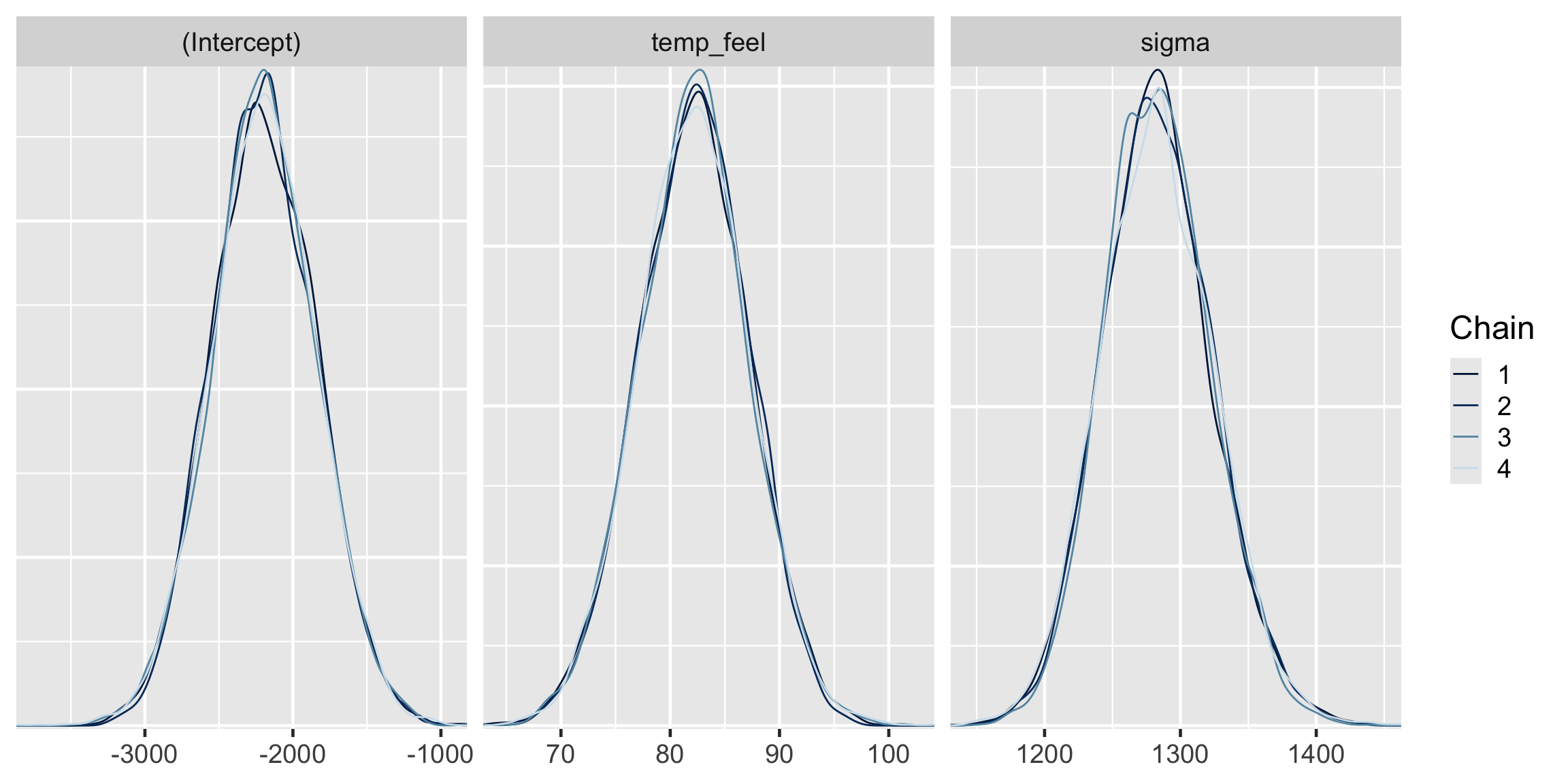
# A tibble: 4 × 5
  term        estimate std.error conf.low conf.high
  <chr>          <dbl>     <dbl>    <dbl>     <dbl>
1 (Intercept)  -2195.     354.    -2646.    -1736. 
2 temp_feel       82.2      5.07     75.7      88.7
3 sigma         1282.      40.6    1232.     1336. 
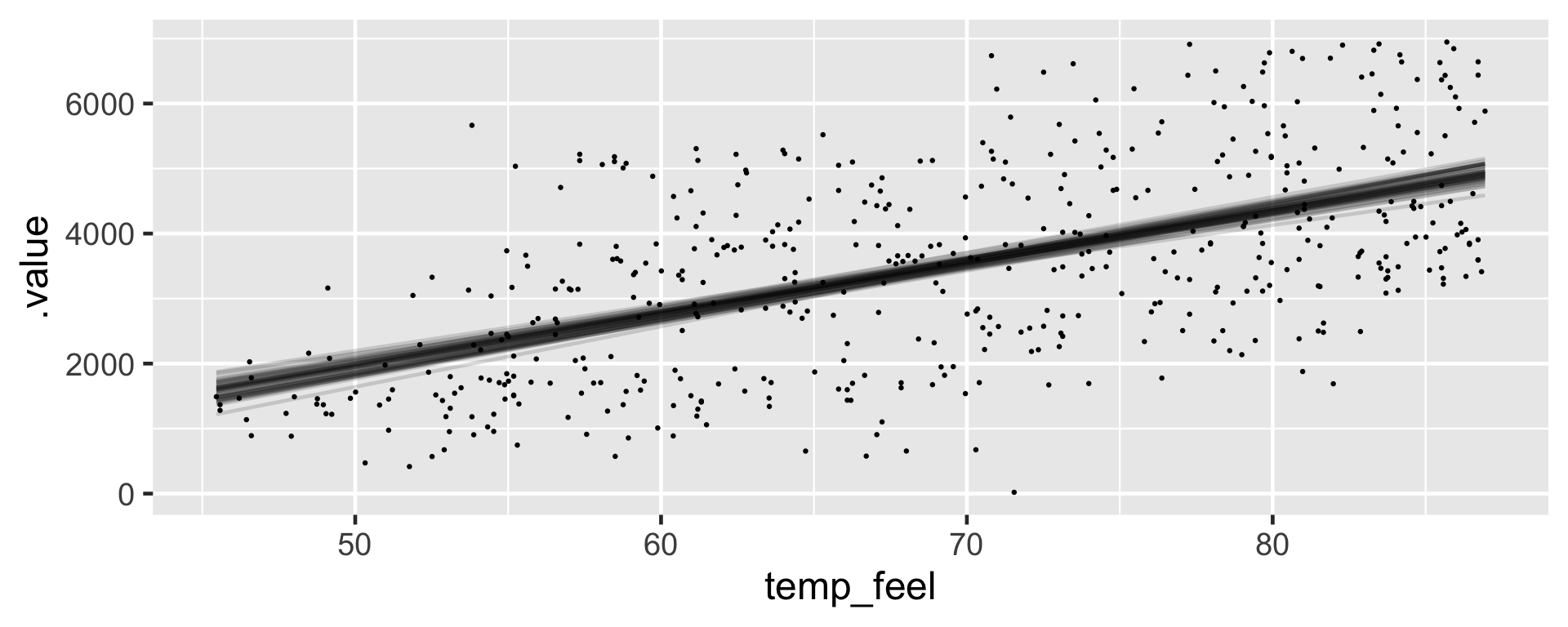
4 mean_PPD      3487.      81.5    3382.     3593.

Referring to the tidy() summary, the posterior median relationship is

\[\begin{equation} -2195.31 + 82.22 X \end{equation}\]

# Store the 4 chains for each parameter in 1 data frame
bike_model_df <- as.data.frame(bike_model)
# Check it out
nrow(bike_model_df)
[1] 20000
head(bike_model_df, 3)
  (Intercept) temp_feel    sigma
1   -2125.091  80.92653 1230.511
2   -2087.977  80.60855 1200.141
3   -2265.712  83.64980 1365.039

# 50 simulated model lines
bikes %>%
  tidybayes::add_fitted_draws(bike_model, n = 50) %>%
  ggplot(aes(x = temp_feel, y = rides)) +
    geom_line(aes(y = .value, group = .draw), alpha = 0.15) + 
    geom_point(data = bikes, size = 0.05)

# Tabulate the beta_1 values that exceed 0
bike_model_df %>% 
  mutate(exceeds_0 = temp_feel > 0) %>% 
  tabyl(exceeds_0)
 exceeds_0     n percent
      TRUE 20000       1

Posterior Prediction

Suppose a weather report indicates that tomorrow will be a 75-degree day in D.C. What’s your posterior guess of the number of riders that Capital Bikeshare should anticipate?

Your natural first crack at this question might be to plug the 75-degree temperature into the posterior median model. Thus, we expect that there will be 3971 riders tomorrow:

\[-2195.31 + 82.22\times75 = 3971.19\]

Not quiet.

Recall that this singular prediction ignores two potential sources of variability:

  • Sampling variability in the data
    The observed ridership outcomes, \(Y\), typically deviate from the model line. That is, we don’t expect every 75-degree day to have the same exact number of rides.
  • Posterior variability in parameters \((\beta_0, \beta_1, \sigma)\)

The posterior median model is merely the center in a range of plausible model lines \(\beta_0 + \beta_1 X\). We should consider this entire range as well as that in \(\sigma\), the degree to which observations might deviate from the model lines.

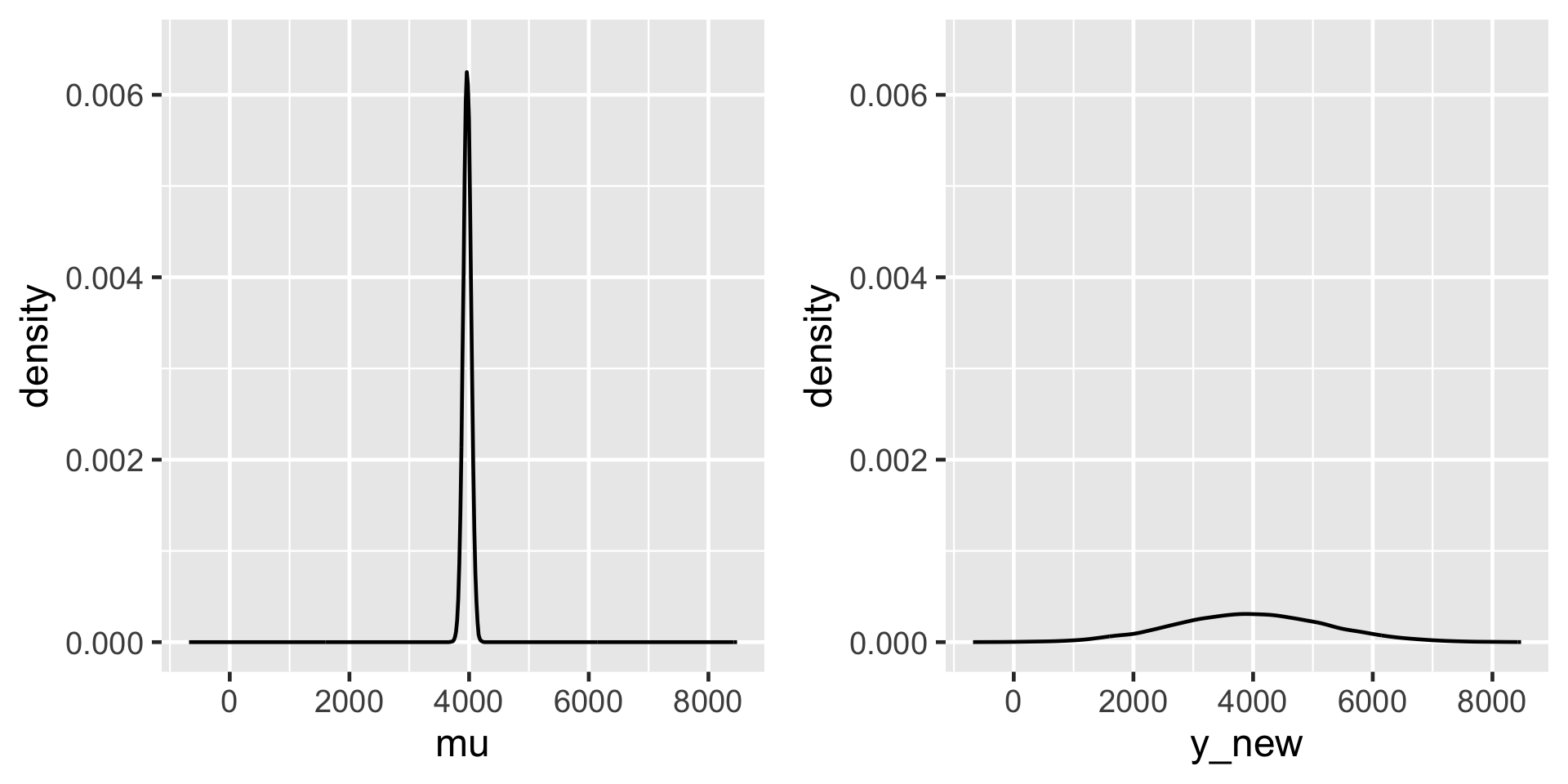
The posterior predictive model of a new data point \(Y_{\text{new}}\) accounts for both sources of variability.

We have20,000 sets of parameters in the Markov chain \(\left(\beta_0^{(i)},\beta_1^{(i)},\sigma^{(i)}\right)\). We can then approximate the posterior predictive model for \(Y_{\text{new}}\) at \(X = 75\) by simulating a ridership prediction from the Normal model evaluated each parameter set:

\[Y_{\text{new}}^{(i)} | \beta_0, \beta_1, \sigma \; \sim \; N\left(\mu^{(i)}, \left(\sigma^{(i)}\right)^2\right) \;\; \text{ with } \;\; \mu^{(i)} = \beta_0^{(i)} + \beta_1^{(i)} \cdot 75.\]

\[\left[ \begin{array}{lll} \beta_0^{(1)} & \beta_1^{(1)} & \sigma^{(1)} \\ \beta_0^{(2)} & \beta_1^{(2)} & \sigma^{(2)} \\ \vdots & \vdots & \vdots \\ \beta_0^{(20000)} & \beta_1^{(20000)} & \sigma^{(20000)} \\ \end{array} \right] \;\; \longrightarrow \;\; \left[ \begin{array}{l} Y_{\text{new}}^{(1)} \\ Y_{\text{new}}^{(2)} \\ \vdots \\ Y_{\text{new}}^{(20000)} \\ \end{array} \right]\]

first_set <- head(bike_model_df, 1)
first_set
  (Intercept) temp_feel    sigma
1   -2125.091  80.92653 1230.511

mu <- first_set$`(Intercept)` + first_set$temp_feel * 75
mu
[1] 3944.398

set.seed(84735)
y_new <- rnorm(1, mean = mu, sd = first_set$sigma)
y_new
[1] 4765.436

# Predict rides for each parameter set in the chain
set.seed(84735)
predict_75 <- bike_model_df %>% 
  mutate(mu = `(Intercept)` + temp_feel*75,
         y_new = rnorm(20000, mean = mu, sd = sigma))
head(predict_75, 3)
  (Intercept) temp_feel    sigma       mu    y_new
1   -2125.091  80.92653 1230.511 3944.398 4765.436
2   -2087.977  80.60855 1200.141 3957.664 3809.038
3   -2265.712  83.64980 1365.039 4008.023 5073.938

# Construct 95% posterior credible intervals
predict_75 %>% 
  summarize(lower_mu = quantile(mu, 0.025),
            upper_mu = quantile(mu, 0.975),
            lower_new = quantile(y_new, 0.025),
            upper_new = quantile(y_new, 0.975))
  lower_mu upper_mu lower_new upper_new
1 3841.078 4096.946  1492.331  6502.669

# Plot the posterior model of the typical ridership on 75 degree days
ggplot(predict_75, aes(x = mu)) + 
  geom_density()
# Plot the posterior predictive model of tomorrow's ridership
ggplot(predict_75, aes(x = y_new)) + 
  geom_density()

Posterior Prediction with rstanarm

# Simulate a set of predictions
set.seed(84735)
shortcut_prediction <- 
  posterior_predict(bike_model, newdata = data.frame(temp_feel = 75))
head(shortcut_prediction, 3)
            1
[1,] 4765.436
[2,] 3809.038
[3,] 5073.938

# Construct a 95% posterior credible interval
posterior_interval(shortcut_prediction, prob = 0.95)
      2.5%    97.5%
1 1492.331 6502.669

# Plot the approximate predictive model
mcmc_dens(shortcut_prediction) + 
  xlab("predicted ridership on a 75 degree day")

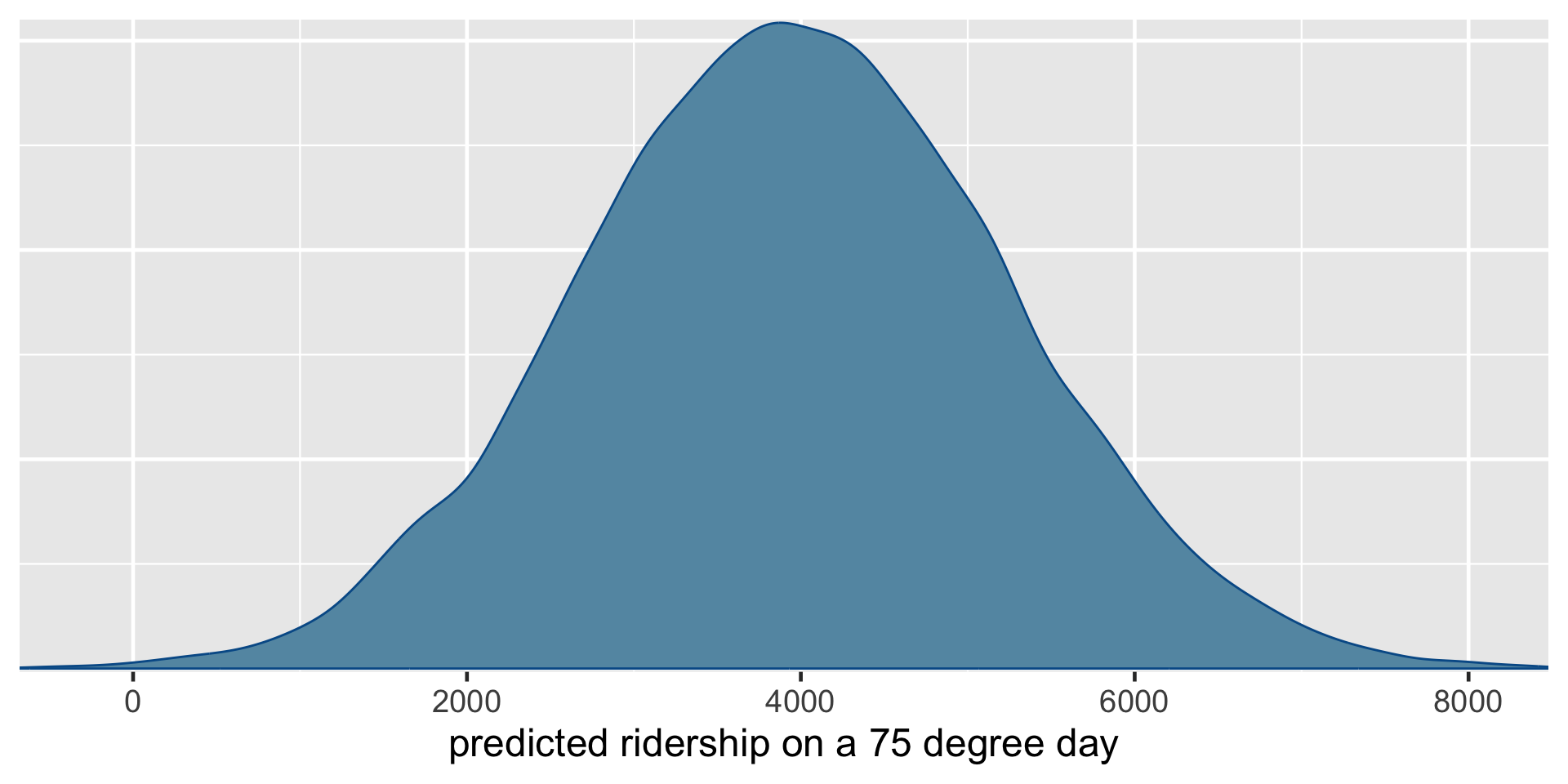
Using the default priors in rstanarm

bike_model_default <- stan_glm(
  rides ~ temp_feel, data = bikes, 
  family = gaussian,
  prior_intercept = normal(5000, 2.5, autoscale = TRUE),
  prior = normal(0, 2.5, autoscale = TRUE), 
  prior_aux = exponential(1, autoscale = TRUE),
  chains = 4, iter = 5000*2, seed = 84735, refresh=FALSE)

By setting autoscale = TRUE, stan_glm() adjusts or scales our default priors to optimize the study of parameters which have different scales.

prior_summary(bike_model_default)
Priors for model 'bike_model_default' 
------
Intercept (after predictors centered)
  Specified prior:
    ~ normal(location = 5000, scale = 2.5)
  Adjusted prior:
    ~ normal(location = 5000, scale = 3937)

Coefficients
  Specified prior:
    ~ normal(location = 0, scale = 2.5)
  Adjusted prior:
    ~ normal(location = 0, scale = 351)

Auxiliary (sigma)
  Specified prior:
    ~ exponential(rate = 1)
  Adjusted prior:
    ~ exponential(rate = 0.00064)
------
See help('prior_summary.stanreg') for more details

Default vs non-default priors

Con: weakly informative priors are tuned with information from the data (through a fairly minor consideration of scale).

Pro: Unless we have strong prior information, utilizing the defaults will typically lead to more stable simulation results than if we tried tuning our own vague priors.

Pro: The defaults can help us get up and running with Bayesian modeling. In future lectures, we’ll often utilize the defaults in order to focus on the new modeling concepts.