Simple Linear Regression

Dr. Mine Dogucu

Data babies in openintro package

Rows: 1,236
Columns: 8
$ case      <int> 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 1…
$ bwt       <int> 120, 113, 128, 123, 108, 136, 138, 132, 120, 143, 140, 144, …
$ gestation <int> 284, 282, 279, NA, 282, 286, 244, 245, 289, 299, 351, 282, 2…
$ parity    <int> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, …
$ age       <int> 27, 33, 28, 36, 23, 25, 33, 23, 25, 30, 27, 32, 23, 36, 30, …
$ height    <int> 62, 64, 64, 69, 67, 62, 62, 65, 62, 66, 68, 64, 63, 61, 63, …
$ weight    <int> 100, 135, 115, 190, 125, 93, 178, 140, 125, 136, 120, 124, 1…
$ smoke     <int> 0, 0, 1, 0, 1, 0, 0, 0, 0, 1, 0, 1, 1, 1, 0, 0, 1, 1, 0, 1, …

Baby Weights

ggplot(babies, 
       aes(x = gestation, y = bwt)) +
  geom_point()

Baby Weights

ggplot(babies,
       aes(x = gestation, y = bwt)) +
  geom_point() +
  geom_smooth(method = "lm", se = FALSE)

lm stands for linear model
se stands for standard error

y Response Birth weight Numeric
x Explanatory Gestation Numeric

Linear Equations Review

Recall from your previous math classes

\(y = mx + b\)

where \(m\) is the slope and \(b\) is the y-intercept

e.g. \(y = 2x -1\)

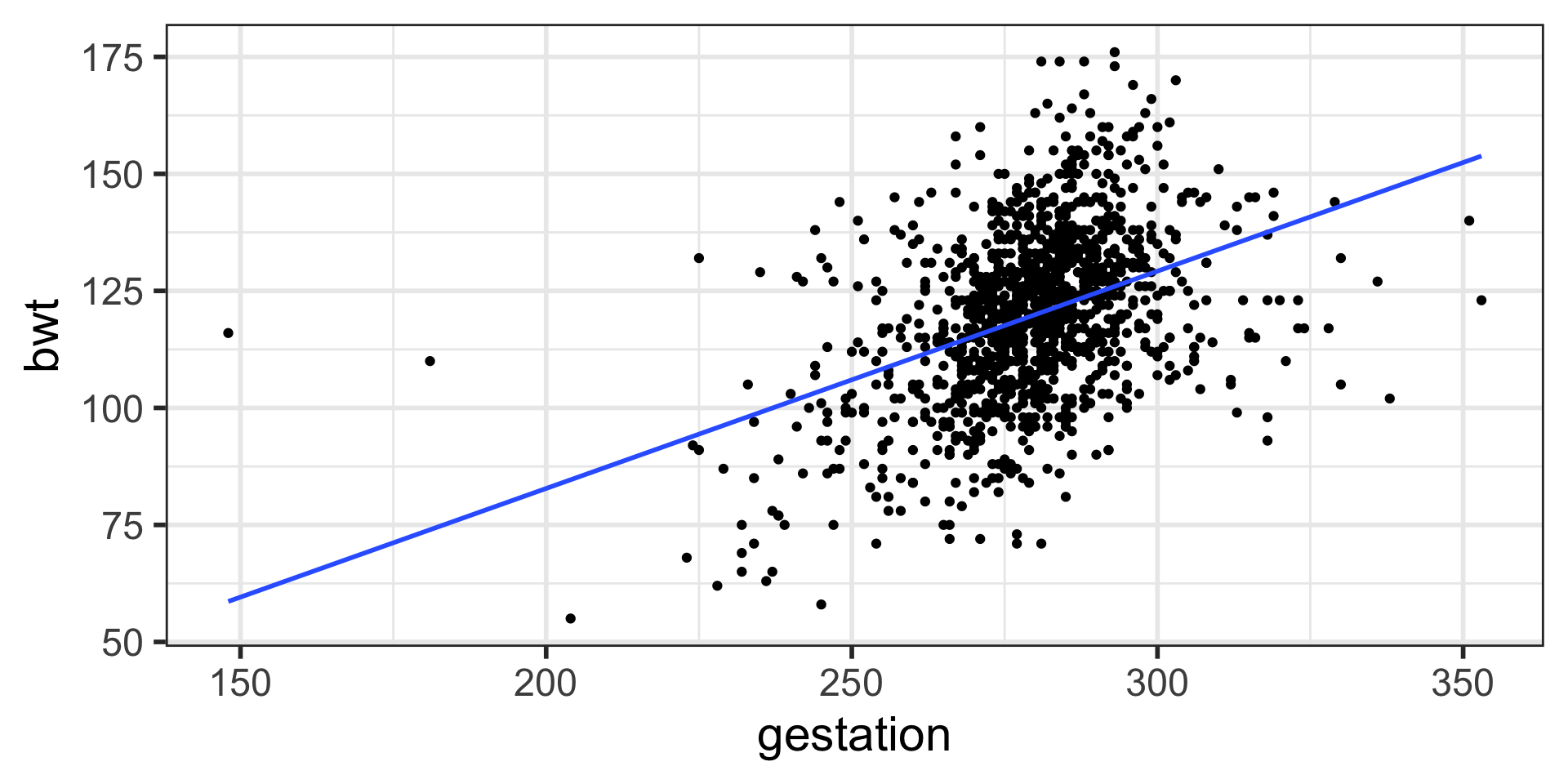
Notice anything different between baby weights plot and this one?

Math class

\(y = b + mx\)

\(b\) is y-intercept
\(m\) is slope

Stats class

\(y_i = \beta_0 +\beta_1x_i + \epsilon_i\)

\(\beta_0\) is y-intercept
\(\beta_1\) is slope
\(\epsilon_i\) is error/residual
\(i = 1, 2, ...n\) identifier for each point

Notation

Sample Statistic Population Parameter
Intercept \(b_0\) \(\beta_0\)
Slope \(b_1\) \(\beta_1\)
Error/Residual \(e\) \(\epsilon\) 

model_g <- lm(bwt ~ gestation, data = babies)

lm stands for linear model. We are fitting a linear regression model. Note that the variables are entered in y ~ x order.

broom::tidy(model_g)
# A tibble: 2 × 5
  term        estimate std.error statistic  p.value
  <chr>          <dbl>     <dbl>     <dbl>    <dbl>
1 (Intercept)  -10.1      8.32       -1.21 2.27e- 1
2 gestation      0.464    0.0297     15.6  3.22e-50

\(\hat {y}_i = b_0 + b_1 x_i\)

\(\hat {\text{bwt}_i} = b_0 + b_1 \text{ gestation}_i\)

\(\hat {\text{bwt}_i} = -10.1 + 0.464\text{ gestation}_i\)

Expected bwt for a baby with 300 days of gestation

\(\hat {\text{bwt}_i} = -10.1 + 0.464\text{ gestation}_i\)

\(\hat {\text{bwt}} = -10.1 + 0.464 \times 300\)

\(\hat {\text{bwt}} =\) 129.1

For a baby with 300 days of gestation the expected birth weight is 129.1 ounces.

Interpretation of estimates

\(b_1 = 0.464\) which means for one unit(day) increase in gestation period the expected increase in birth weight is 0.464 ounces.

\(b_0 = -10.1\) which means for gestation period of 0 days the expected birth weight is -10.1 ounces!!!!!!!! (does NOT make sense)

Extrapolation

  • There is no such thing as 0 days of gestation.
  • Birth weight cannot possibly be -10.1 ounces.
  • Extrapolation happens when we use a model outside the range of the x-values that are observed. After all, we cannot really know how the model behaves (e.g. may be non-linear) outside of the scope of what we have observed.

Baby number 148

babies %>% 
  filter(case == 148) %>% 
  select(bwt, gestation)
# A tibble: 1 × 2
    bwt gestation
  <int>     <int>
1   160       300

Baby #148

Expected

\(\hat y_{148} = b_0 +b_1x_{148}\)

\(\hat y_{148} = -10.1 + 0.464\times300\)

\(\hat y_{148}\) = 129.1

Observed

\(y_{148} =\) 160

Residual for i = 148

\(y_{148} = 160\)

\(\hat y_{148}\) = 129.1

\(e_{148} = y_{148} - \hat y_{148}\)

\(e_{148} =\) 30.9

Least Squares Regression

The goal is to minimize

\[e_1^2 + e_2^2 + ... + e_n^2\]

which can be rewritten as

\[\sum_{i = 1}^n e_i^2\]

Conditions

Conditions for Least Squares Regression

  • Linearity

  • Normality of Residuals

  • Constant Variance

  • Independence

Linear

Non-linear

Nearly normal

Not normal

Constant Variance

Non-constant variance

Independence

Harder to check because we need to know how the data were collected.

In the description of the dataset it says [a study]considered all pregnancies between 1960 and 1967 among women in the Kaiser Foundation Health Plan in the San Francisco East Bay area.

It is possible that babies born in the same hospital may have similar birth weight.

Correlated data examples: patients within hospitals, students within schools, people within neighborhoods, time-series data.

Inference

Inference: Hypothesis Testing

\(H_o: \beta_1 = 0\)

\(H_A: \beta_1 \neq 0\)

tidy(model_g)
# A tibble: 2 × 5
  term        estimate std.error statistic  p.value
  <chr>          <dbl>     <dbl>     <dbl>    <dbl>
1 (Intercept)  -10.1      8.32       -1.21 2.27e- 1
2 gestation      0.464    0.0297     15.6  3.22e-50

Since the p-value of 3.22e-50 < 0.05 we reject the null hypothesis and conclude that there is a significant relationship between gestation and birth weight.

Inference: Confidence Interval

CI = point estimate \(\pm\) critical value \(\times\) standard error

95% CI for the slope = point estimate of the slope \(\pm\) critical value \(\times\) standard error of the slope

Critical value

qt(0.975, df = 1235) # recall n = 1236
[1] 1.961887

Inference: Confidence Interval

tidy(model_g)
# A tibble: 2 × 5
  term        estimate std.error statistic  p.value
  <chr>          <dbl>     <dbl>     <dbl>    <dbl>
1 (Intercept)  -10.1      8.32       -1.21 2.27e- 1
2 gestation      0.464    0.0297     15.6  3.22e-50

95% CI = 0.4642626 \(\pm\) 1.9618867 \(\times\) 0.0297437

95% CI = (0.4059089, 0.5226163)

Inference: Confidence Interval

tidy(model_g)
# A tibble: 2 × 5
  term        estimate std.error statistic  p.value
  <chr>          <dbl>     <dbl>     <dbl>    <dbl>
1 (Intercept)  -10.1      8.32       -1.21 2.27e- 1
2 gestation      0.464    0.0297     15.6  3.22e-50

Inference: Confidence Interval

confint(model_g)
                  2.5 %    97.5 %
(Intercept) -26.3915884 6.2632199
gestation     0.4059083 0.5226169

Note that the 95% confidence interval for the slope does not contain zero and all the values in the interval are positive indicating a significant positive relationship between gestation and birth weight.

Confidence Interval

y Response Birth weight Numeric
x Explanatory Smoke Categorical

Notation

\(y_i = \beta_0 +\beta_1x_i + \epsilon_i\)

\(\beta_0\) is y-intercept
\(\beta_1\) is slope
\(\epsilon_i\) is error/residual
\(i = 1, 2, ...n\) identifier for each point

model_s <- lm(bwt ~ smoke, data = babies)
tidy(model_s)
# A tibble: 2 × 5
  term        estimate std.error statistic  p.value
  <chr>          <dbl>     <dbl>     <dbl>    <dbl>
1 (Intercept)   123.       0.649    190.   0       
2 smoke          -8.94     1.03      -8.65 1.55e-17

\(\hat {y}_i = b_0 + b_1 x_i\)

\(\hat {\text{bwt}_i} = b_0 + b_1 \text{ smoke}_i\)

\(\hat {\text{bwt}_i} = 123 + (-8.94\text{ smoke}_i)\)

Expected bwt for a baby with a non-smoker mother

\(\hat {\text{bwt}_i} = 123 + (-8.94\text{ smoke}_i)\)

\(\hat {\text{bwt}_i} = 123 + (-8.94\times 0)\)

\(\hat {\text{bwt}_i} = 123\)

\(E[bwt_i | smoke_i = 0] = b_0\)

Expected bwt for a baby with a smoker mother

\(\hat {\text{bwt}_i} = 123 + (-8.94\text{ smoke}_i)\)

\(\hat {\text{bwt}_i} = 123 + (-8.94\times 1)\)

\(\hat {\text{bwt}_i} = 114.06\)

\(E[bwt_i | smoke_i = 1] = b_0 + b_1\)

confint(model_s)
                2.5 %     97.5 %
(Intercept) 121.77391 124.320430
smoke       -10.96413  -6.911199

Note that the confidence interval for the “slope” does not contain 0 and all the values in the interval are negative.

Understanding Relationships

  • Just because we observe a significant relationship between \(x\) and \(y\), it does not mean that \(x\) causes \(y\).

  • Just because we observe a significant relationship in a sample that does not mean the findings will generalize to the population.

  • For these we need to understand sampling and study design.

stats4cs.com